
【題目】2015年10月十八屆五中全會決定2016年1月1日起全國統一實施全面兩孩政策,為了了解適齡民眾對放開生育二胎政策的態度,某市進行了一次民意調查,參與調查的100位市民中,年齡分布情況如下圖所示,并得到適齡民眾對放開生育二胎政策的態度數據如下表:
生二胎 | 不生二胎 | 合計 | |
25~35歲 | 10 | ||
35~50歲 | 30 | ||
合計 | 100 |
(1)填寫上面的![]() 列聯表;
列聯表;
(2)根據調查數據,有多少的把握認為“生二胎與年齡有關”,說明理由;
(3)調查對象中決定生二胎的民眾有六人分別來自三個不同的家庭且為父子,各自家庭都有一個約定:父親先生二胎,然后兒子生二胎,則這三個家庭“二胎出生的日期的先后順序”有多少種?
參考數據:
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
(參考公式:![]() ,其中
,其中![]() )
)
【答案】(1)見解析;(2)有90% 以上的把握認為“生二胎與年齡有關”;(3)![]() .
.
【解析】
試題分析:(1)根據題意,填寫![]() 列聯表即可;
列聯表即可;
(2)根據調查數據計算![]() ,對照數表即可得出結論;
,對照數表即可得出結論;
(3)分別計算三對父子的二胎出生日期僅為不同的二天、不同的三天、不同的四天、不同的五天和不同的六天時的種數,求和即可.
試題解析:
解:(1)
| 生二胎 | 不生二胎 | 合計 |
25~35歲 | (45) | 10 | (55) |
35~50歲 | 30 | (15) | (45) |
合計 | (75) | (25) | 100 |
-------3分
(2)![]() -7分
-7分
所以有90% 以上的把握認為“生二胎與年齡有關”-------------8分
(3)(以前的答案有誤)三對父子的二胎出生日期僅為不同的二天,則有1種;
三對父子的二胎出生日期僅為不的三天,則有![]() 種; --------9分
種; --------9分
三對父子的二胎出生日期僅為不同的四天,則有![]() 種;10分
種;10分
三對父子的二胎出生日期僅為不同的五天,則有
![]() 種; --------11分
種; --------11分
三對父子的二胎出生日期僅為不同的六天,則有
![]() 或
或![]() 種.
種.
故共計![]() 種 ----12分
種 ----12分
(后四種每寫對一種得1分)


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin![]() -2
-2![]() ·sin2x.
·sin2x.
(1) 求函數f(x)的最小正周期;
(2) 求函數f(x)圖象的對稱軸方程、對稱中心的坐標;
(3) 當0≤x≤![]() 時,求函數f(x)的最大、最小值.
時,求函數f(x)的最大、最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三個元素,分別作為一個三位數的個位數,十位數和百位數,記這個三位數為a,現將組成a的三個數字按從小到大排成的三位數記為I(a),按從大到小排成的三位數記為D(a)(例如a=219,則I(a)=129,D(a)=921),閱讀如圖所示的程序框圖,運行相應的程序,任意輸入一個a,則輸出b的值為( )
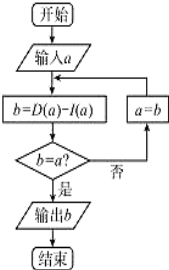
A.792 B.693
C.594 D.495
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓C上.
在橢圓C上.
(1)求橢圓C的方程;
(2)設動直線![]() 與橢圓C有且僅有一個公共點,判斷是否存在以原點O為圓心的圓,滿足此圓與
與橢圓C有且僅有一個公共點,判斷是否存在以原點O為圓心的圓,滿足此圓與![]() 相交兩點
相交兩點![]() ,
,![]() (兩點均不在坐標軸上),且使得直線
(兩點均不在坐標軸上),且使得直線![]() ,
,![]() 的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業開發一種新產品,現準備投入適當的廣告費,對產品進行促銷,在一年內,預計年銷量Q(萬件)與廣告費x(萬件)之間的函數關系為![]() ,已知生產此產品的年固定投入為3萬元,每年產1萬件此產品仍需要投入32萬元,若年銷售額為
,已知生產此產品的年固定投入為3萬元,每年產1萬件此產品仍需要投入32萬元,若年銷售額為![]() ,而當年產銷量相等。
,而當年產銷量相等。
(1)試將年利潤P(萬件)表示為年廣告費x(萬元)的函數;
(2)當年廣告費投入多少萬元時,企業年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為
,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為![]() .
.
(1)求橢圓![]() 的方程式;
的方程式;
(2)已知動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點.
兩點.
①若線段![]() 中點的橫坐標為
中點的橫坐標為![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知點![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照![]() ,…,
,…,![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
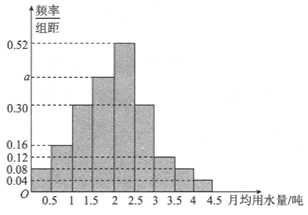
(1)求直方圖中![]() 的值;
的值;
(2)若該市有110萬居民,估計全市居民中月均用水量不低于3噸的人數,請說明理由;
(3)估計居民月均用水量的中位數(精確到0.01)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]() .
.
(1)當![]() ,求函數
,求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)設定義在![]() 上的函數
上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,若
,若![]() 在
在![]() 內恒成立,則稱
內恒成立,則稱![]() 為函數
為函數![]() 的“類對稱點”,當
的“類對稱點”,當![]() 時,試問
時,試問![]() 是否存在“類對稱點”,若存在,請至少求出一個“類對稱點”的橫坐標;若不存在,請說明理由.
是否存在“類對稱點”,若存在,請至少求出一個“類對稱點”的橫坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com