
【題目】從拋物線![]() 上任意一點P向x軸作垂線段,垂足為Q,點M是線段
上任意一點P向x軸作垂線段,垂足為Q,點M是線段![]() 上的一點,且滿足
上的一點,且滿足![]()
(1)求點M的軌跡C的方程;
(2)設直線![]() 與軌跡c交于
與軌跡c交于![]() 兩點,T為C上異于
兩點,T為C上異于![]() 的任意一點,直線
的任意一點,直線![]() ,
,![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點,以
兩點,以![]() 為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
【答案】(1) ![]() (2)見解析
(2)見解析
【解析】
(1)利用相關點法,設設![]() ,
,![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,由
,由![]() ,從而得到
,從而得到![]() ,即
,即![]() .化簡求得結果;
.化簡求得結果;
(2)設出點A,B的坐標,將直線與曲線的方程聯立,消元得到![]() ,根據韋達定理得到
,根據韋達定理得到![]()
![]() =
=![]() ,
,![]()
![]() =
=![]() ,設點
,設點![]() ,寫出直線AT的方程,進而求得點D的坐標,同理求得點E的坐標,如果以
,寫出直線AT的方程,進而求得點D的坐標,同理求得點E的坐標,如果以![]() 為直徑的圓過
為直徑的圓過![]() 軸某一定點
軸某一定點![]() ,則滿足
,則滿足![]() ,利用向量數量積坐標公式求得結果.
,利用向量數量積坐標公式求得結果.
(1)設![]() ,
,![]() ,則點
,則點![]() 的坐標為
的坐標為![]() .
.
因為![]() ,
,
所以![]() ,
,
即![]() ,
,
因為點![]() 在拋物線
在拋物線![]() 上,
上,
所以![]() ,即
,即![]() .
.
所以點![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]() .
.
(2)解法1:設直線![]() 與曲線
與曲線![]() 的交點坐標為
的交點坐標為![]()
![]() ,
,![]() ,
,
由![]() 得
得![]() .
.
由韋達定理得![]()
![]() =
=![]() ,
,![]()
![]() =
=![]() .
.
設點![]() ,則
,則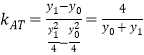 .
.
所以直線![]() 的方程為
的方程為![]() .
.
令![]() ,得點
,得點![]() 的坐標為
的坐標為![]() .
.
同理可得點![]() 的坐標為
的坐標為![]() .
.
如果以![]() 為直徑的圓過
為直徑的圓過![]() 軸某一定點
軸某一定點![]() ,則滿足
,則滿足![]() .
.
因為![]()
![]() .
.
所以![]() .
.
即![]() ,解得
,解得![]() 或
或![]() .
.
故以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() 和
和![]() .
.
解法2:直線![]() 與曲線
與曲線![]() 的交點坐標為
的交點坐標為![]() ,
,![]() ,
,
若取![]() ,則
,則![]() ,
,![]() 與直線
與直線![]() 的交點坐標為
的交點坐標為![]() ,
,![]() ,
,
所以以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() .
.
該圓與![]() 軸的交點坐標為
軸的交點坐標為![]() 和
和![]() .
.
所以符合題意的定點只能是![]() 或
或![]() .
.
設直線![]() 與曲線
與曲線![]() 的交點坐標為
的交點坐標為![]()
![]() ,
,![]() ,
,
由![]() 得
得![]() .
.
由韋達定理得![]()
設點![]() ,則
,則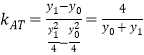 .
.
所以直線![]() 的方程為
的方程為![]() .
.
令![]() ,得點
,得點![]() 的坐標為
的坐標為![]() .
.
同理可得點![]() 的坐標為
的坐標為![]() .
.
若點![]() 滿足要求,則滿足
滿足要求,則滿足![]() .
.
因為![]()
![]()
![]() .
.
所以點![]() 滿足題意.
滿足題意.
同理可證點![]() 也滿足題意.
也滿足題意.
故以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() 和
和![]() .
.


 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數學 來源: 題型:
【題目】已數列![]() 的各項均為正整數,且滿足
的各項均為正整數,且滿足![]() ,又
,又![]() .
.
(1)求![]() 的值,猜想
的值,猜想![]() 的通項公式并用數學歸納法證明;
的通項公式并用數學歸納法證明;
(2)設![]() ,求
,求![]() 的值;
的值;
(3)設![]() ,是否存在最大的整數
,是否存在最大的整數![]() ,使得對任意
,使得對任意![]() ,均有
,均有![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xex-alnx(無理數e=2.718…).
(1)若f(x)在(0,1)單調遞減,求實數a的取值范圍;
(2)當a=-1時,設g(x)=x(f(x)-xex)-x3+x2-b,若函數g(x)存在零點,求實數b的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科研人員在對人體脂肪含量和年齡之間關系的研究中,獲得了一些年齡和脂肪含量的簡單隨機樣本數據,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根據上表的數據得到如下的散點圖.
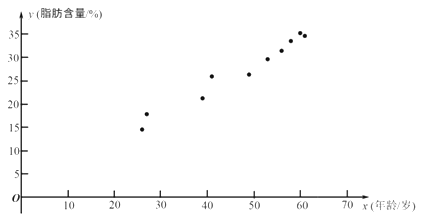
(1)根據上表中的樣本數據及其散點圖:
(i)求![]() ;
;
(i)計算樣本相關系數(精確到0.01),并刻畫它們的相關程度.
(2)若![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,求
,求![]() 的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
附:參考數據:img src="http://thumb.zyjl.cn/Upload/2019/08/18/08/786210e5/SYS201908180802150104289801_ST/SYS201908180802150104289801_ST.007.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數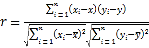
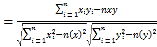
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為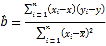 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 為拋物線
為拋物線![]() 的焦點,過點
的焦點,過點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,點
兩點,點![]() 在拋物線上,使得
在拋物線上,使得![]() 的重心
的重心![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() 在點
在點![]() 的右側.記
的右側.記![]() 、
、![]() 的面積分別
的面積分別![]() 、
、![]() .
.

(1)求![]() 的值及拋物線的方程;
的值及拋物線的方程;
(2)求![]() 的最小值及此時點
的最小值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com