
【題目】已知函數 ![]() ,若滿足f(1)=
,若滿足f(1)= ![]()
(1)求實數a的值;
(2)證明:f(x)為奇函數.
(3)判斷并證明函數f(x)的單調性.
【答案】
(1)解:f(1)= ![]() ;
;
∴ ![]() ;
;
∴a=1
(2)解:證明: ![]() ;
;
該函數定義域為R,f(﹣x)= ![]() ;
;
∴f(x)為奇函數
(3)解: ![]() ,可看出x增大時,f(x)增大,∴f(x)在R上為增函數,證明如下:
,可看出x增大時,f(x)增大,∴f(x)在R上為增函數,證明如下:
設x1,x2∈R,且x1<x2,則:
![]() =
= ![]() ;
;
∵x1<x2;
∴ ![]() ,
, ![]() ;
;
∴f(x1)<f(x2);
∴f(x)在R上為增函數
【解析】(1)根據f(1)= ![]() 便可求出a=1;(2)寫出
便可求出a=1;(2)寫出 ![]() ,定義域顯然為R,容易得到f(﹣x)=﹣f(x),從而得出該函數為奇函數;(3)分離常數得到
,定義域顯然為R,容易得到f(﹣x)=﹣f(x),從而得出該函數為奇函數;(3)分離常數得到 ![]() ,根據單調性定義便可判斷該函數在R上單調遞增,根據增函數的定義證明:設任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根據指數函數的單調性證明f(x1)<f(x2)即可得出f(x)在R上單調遞增.
,根據單調性定義便可判斷該函數在R上單調遞增,根據增函數的定義證明:設任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根據指數函數的單調性證明f(x1)<f(x2)即可得出f(x)在R上單調遞增.
【考點精析】利用函數單調性的判斷方法和函數奇偶性的性質對題目進行判斷即可得到答案,需要熟知單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較;在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇.


科目:高中數學 來源: 題型:
【題目】如圖,正方形ADEF與梯形ABCD所在的閏面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M為CE的中點.
(1)求證:BM∥平面ADEF;
(2)求平面BEC與平面ADEF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)設函數h(x)=g(x)﹣f(x),求函數h(x)在區間[2,4]上的值域;
(2)定義min(p,q)表示p,q中較小者,設函數H(x)=min{f(x),g(x)}(x>0), ①求函數H(x)的單調區間及最值;
②若關于x的方程H(x)=k有兩個不同的實根,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,其左頂點
,其左頂點![]() 在圓
在圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,設點
兩點,設點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() (點
(點![]() 與點
與點![]() 不重合),且直線
不重合),且直線![]() 與
與![]() 軸的交于點
軸的交于點![]() ,試問
,試問![]() 的面積是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
的面積是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ) 當a=0時,求曲線f(x)在x =1處的切線方程;
(Ⅱ) 設函數![]() ,求函數h(x)的極值;
,求函數h(x)的極值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一點x0,使得
在[1,e](e=2.718 28…)上存在一點x0,使得![]() 成立,求a的取值范圍.
成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年年底,某商業集團根據相關評分標準,對所屬20家商業連鎖店進行了年度考核評估,并依據考核評估得分(最低分60分,最高分100分)將這些連鎖店分別評定為A,B,C,D四個類型,其考核評估標準如下表:
評估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
評分類型 | D | C | B | A |
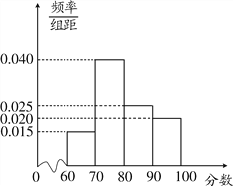 考核評估后,對各連鎖店的評估分數進行統計分析,得其頻率分布直方圖如下:
考核評估后,對各連鎖店的評估分數進行統計分析,得其頻率分布直方圖如下:
(Ⅰ)評分類型為A的商業連鎖店有多少家;
(Ⅱ)現從評分類型為A,D的所有商業連鎖店中隨機抽取兩家做分析,求這兩家來自同一評分類型的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是矩形,側棱PD⊥底面ABCD,PD=DC,點E是PC的中點,作EF⊥PB交PB于點F. 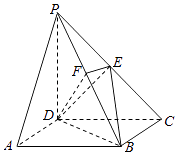
(1)求證:PA∥平面BDE;
(2)求證:PB⊥平面DEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列命題:
①乘積(a+b+c+d)(p+q+r)(m+n)展開式的項數是24;
②由1、2、3、4、5組成沒有重復數字且1、2都不與5相鄰的五位數的個數是36;
③某會議室第一排共有8個座位,現有3人就座,若要求每人左右均有空位,那么不同的坐法種數為24;
④已知(1+x)8=a0+a1x+…+a8x8 , 其中a0 , a1 , …,a8中奇數的個數為2.
其中真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列結論: ①已知函數f(x)是定義在R上的奇函數,若f(﹣1)=2,f(﹣3)=﹣1,則f(3)<f(﹣1);
②函數y=log ![]() (x2﹣2x)的單調遞增減區間是(﹣∞,0);
(x2﹣2x)的單調遞增減區間是(﹣∞,0);
③已知函數f(x)是奇函數,當x≥0時,f(x)=x2 , 則當x<0時,f(x)=﹣x2;
④若函數y=f(x)的圖象與函數y=ex的圖象關于直線y=x對稱,則對任意實數x,y都有f(xy)=f(x)+f(y).
則正確結論的序號是(請將所有正確結論的序號填在橫線上).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com