【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c，sin2A+sin2B+sin2C=2 
sinAsinBsinC，且a=2，則△ABC的外接圓半徑R= ．
【答案】
【解析】解：由正弦定理可化sin2A+sin2B+sin2C=2 
sinAsinBsinC為a2+b2+c2=2 absinC，再由余弦定理可得c2=a2+b2﹣2abcosC，代入上式可得2（a2+b2）=2 absinC+2abcosC，
∴2（a2+b2）=4ab（ 
sinC+ 
cosC）=4absin（C+ 
），
∴a2+b2=2absin（C+ ）≤2ab，
又由基本不等式可得a2+b2≥2ab，∴a2+b2=2ab，
∴（a﹣b）2=0且sin（C+ ）=1，
∴a=b且C= 
，∴△ABC為正三角形，
由正弦定理可得2R= 
= 
= 
，
解得R=
所以答案是：
【考點精析】本題主要考查了正弦定理的定義的相關知識點，需要掌握正弦定理:
才能正確解答此題．
精英口算卡系列答案
應用題點撥系列答案
狀元及第系列答案
同步奧數系列答案科目：高中數學 來源： 題型：
【題目】要得到函數f（x）=2sinxcosx，x∈R的圖象，只需將函數g（x）=2cos2x﹣1，x∈R的圖象（ ）
A.向左平移 
個單位
B.向右平移 個單位
C.向左平移 
個單位
D.向右平移 個單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校數學課外興趣小組為研究數學成績是否與性別有關，先統計本校高三年級每個學生一學期數學成績平均分(采用百分制)，剔除平均分在40分以下的學生后，共有男生300名，女生200名．現采用分層抽樣的方法，從中抽取了100名學生，按性別分為兩組，并將兩組學生成績分為6組，得到如下所示頻數分布表．
（1）估計男、女生各自的平均分(同一組數據用該組區間中點值作代表)，從計算結果看，數學成績與性別是否有關；
（2）規定80分以上為優分(含80分)，請你根據已知條件作出2×2列聯表，并判斷是否有90%以上的把握認為“數學成績與性別有關”．
附表及公式：
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知極點與直角坐標系的原點重合，極軸與x軸的正半軸重合，圓C的極坐標方程是ρ=asinθ，直線l的參數方程是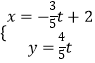 
（t為參數）
（1）若a=2，直線l與x軸的交點是M，N是圓C上一動點，求|MN|的最大值；
（2）直線l被圓C截得的弦長等于圓C的半徑的 
倍，求a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下表是某廠生產某種產品的過程中記錄的幾組數據，其中
表示產量（單位：噸），
表示生產中消耗的煤的數量（單位：噸）.
|
|
|
|
|
|
|
|
|
|
|
|
（1）試在給出的坐標系下作出散點圖，根據散點圖判斷，在
與
中，哪一個方程更適合作為變量關于的回歸方程模型？（給出判斷即可，不需要說明理由）
（2）根據（1）的結果以及表中數據，建立變量關于的回歸方程.并估計生產
噸產品需要準備多少噸煤.參考公式：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解高中生作文成績與課外閱讀量之間的關系，某研究機構隨機抽取了60名高中生，通過問卷調查，得到以下數據：
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
由以上數據，計算得到K2的觀測值k≈9.643，根據臨界值表，以下說法正確的是( )
A. 沒有充足的理由認為課外閱讀量大與作文成績優秀有關
B. 有0.5%的把握認為課外閱讀量大與作文成績優秀有關
C. 有99.9%的把握認為課外閱讀量大與作文成績優秀有關
D. 有99.5%的把握認為課外閱讀量大與作文成績優秀有關
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一商場對每天進店人數和商品銷售件數進行了統計對比，得到如下表格：
其中=1,2,3,4,5,6,7.
(1)以每天進店人數為橫軸，每天商品銷售件數為縱軸，畫出散點圖；
(2)求線性回歸方程；(結果保留到小數點后兩位)
(參考數據：
=3 245, 
=25, 
=15.43, 
=5 075)
(3)預測進店人數為80人時，商品銷售的件數．(結果保留整數)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f′（x）是奇函數f（x）（x∈R）的導函數，f（﹣1）=0，當x＞0時，xf′（x）﹣f（x）＜0，則使得f（x）＞0成立的x的取值范圍是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若n是一個三位正整數，且n的個位數字大于十位數字，十位數字大于百位數字，則稱n為“三位遞增數”(如137,359,567等)．
在某次數學趣味活動中，每位參加者需從所有的“三位遞增數”中隨機抽取1個數，且只能抽取一次．得分規則如下：若抽取的“三位遞增數”的三個數字之積不能被5整除，參加者得0分；若能被5整除，但不能被10整除，得－1分；若能被10整除，得1分．
(1)寫出所有個位數字是5的“三位遞增數”；
(2)若甲參加活動，求甲得分X的分布列和數學期望E(X)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
