
【題目】如圖所示,∠PAQ是村里一個小湖的一角,其中∠PAQ=60°.為了給村民營造豐富的休閑環境,村委會決定在直線湖岸AP與AQ上分別建觀光長廊AB與AC,其中AB是寬長廊,造價是800元/米;AC是窄長廊,造價是400元/米;兩段長廊的總造價預算為12萬元(恰好都用完);同時,在線段BC上靠近點B的三等分點D處建一個表演舞臺,并建水上通道AD(表演舞臺的大小忽略不計),水上通道的造價是600元/米. 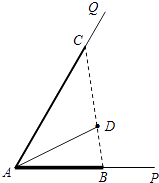
(1)若規劃寬長廊AB與窄長廊AC的長度相等,則水上通道AD的總造價需多少萬元?
(2)如何設計才能使得水上通道AD的總造價最低?最低總造價是多少萬元?
【答案】
(1)解:設AB=AC=x(單位:百米),
則寬長廊造價為8x萬元,窄長廊造價為4x萬元,
故兩段長廊的總造價為12x萬元,所以12x=12,得x=1,
又∠PAQ=60°,△ABC是邊長為1的正三角形,
又點D為線段BC上靠近點B的三等分點,所以BD= ![]() ,
,
在△ABD中,由余弦定理得
AD2=BA2+BD2﹣2BABDcos∠ABD=1+ ![]() ﹣2×
﹣2× ![]() ×
× ![]() =
= ![]() ,即AD=
,即AD= ![]() .
.
又水上通道的造價是6萬元/百米,所以水上通道的總造價為2 ![]() 萬元
萬元
(2)解:設AB=x,AC=y(單位:百米),則兩段長廊的總造價為8x+4y=12,
即2x+y=3,在△ABC中,由余弦定理得:
BC2=AB2+AC2﹣2ABACcos∠BAC=x2+y2﹣2xy ![]() =x2+y2﹣xy,
=x2+y2﹣xy,
在△ABC與△ABD中,由余弦定理及cos∠ABC=cos∠ABD,得
![]() =
= ![]() ,又BC=3BD,
,又BC=3BD,
得AD2= ![]() x2+
x2+ ![]() y2+
y2+ ![]() xy=
xy= ![]() x2+
x2+ ![]() (3﹣2x)2+
(3﹣2x)2+ ![]() x(3﹣2x)=
x(3﹣2x)= ![]() x2﹣
x2﹣ ![]() x+1
x+1
= ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,當且僅當x=
,當且僅當x= ![]() 時,AD有最小值
時,AD有最小值 ![]() ,
,
故總造價有最小值3 ![]() 萬元,此時y=
萬元,此時y= ![]() ,
,
即當寬長廊AB為 ![]() 百米(75米)、窄長廊AC為
百米(75米)、窄長廊AC為 ![]() 百米(150米)時,
百米(150米)時,
水上通道AD有最低總造價為3 ![]() 萬元.
萬元.
【解析】【(1)設AB=AC=x(單位:百米),由題意可得12x=12,即x=1,求得BD= ![]() ,在△ABD中,由余弦定理求得AD的長,即可得到所求造價;(2)設AB=x,AC=y(單位:百米),則兩段長廊的總造價為8x+4y=12,即2x+y=3,y=3﹣2x,運用余弦定理求得BC,再在△ABC與△ABD中,由余弦定理及cos∠ABC=cos∠ABD,求得AD2的解析式,化簡整理,運用配方,即可得到所求最小值,及x,y的值.
,在△ABD中,由余弦定理求得AD的長,即可得到所求造價;(2)設AB=x,AC=y(單位:百米),則兩段長廊的總造價為8x+4y=12,即2x+y=3,y=3﹣2x,運用余弦定理求得BC,再在△ABC與△ABD中,由余弦定理及cos∠ABC=cos∠ABD,求得AD2的解析式,化簡整理,運用配方,即可得到所求最小值,及x,y的值.
【考點精析】解答此題的關鍵在于理解基本不等式在最值問題中的應用的相關知識,掌握用基本不等式求最值時(積定和最小,和定積最大),要注意滿足三個條件“一正、二定、三相等”.


科目:高中數學 來源: 題型:
【題目】學校為測評班級學生對任課教師的滿意度,采用“100分制”打分的方式來計分.現從某班學生中隨機抽取10名,以下莖葉圖記錄了他們對某教師的滿意度分數(以十位數字為莖,個位數字為葉):
規定若滿意度不低于98分,測評價該教師為“優秀”.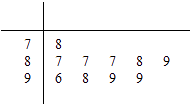
(1)求從這10人中隨機選取3人,至多有1人評價該教師是“優秀”的概率;
記ξ表示抽到評價該教師為“優秀”的人數,求ξ的分布列及數學期望.
(2)以這10人的樣本數據來估計整個班級的總體數據,若從該班任選3人,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=Asin(ωx+)(A,ω,為常數,且A>0,ω>0,0<<π)的部分圖象如圖所示. 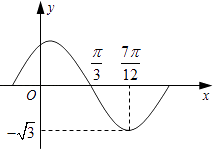
(1)求A,ω,的值;
(2)當x∈[0, ![]() ]時,求f(x)的取值范圍.
]時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的導函數.
(1)若f(x)≥ag(x)恒成立,求實數a的取值范圍;
(2)設n∈N* , 證明: ![]() +
+ ![]() +…+
+…+ ![]() <ln(n+1).
<ln(n+1).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com