
【題目】已知平面直角坐標系內兩定點![]() ,
,![]() 及動點
及動點![]() ,
,![]() 的兩邊
的兩邊![]() 所在直線的斜率之積為
所在直線的斜率之積為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設![]() 是
是![]() 軸上的一點,若(1)中軌跡
軸上的一點,若(1)中軌跡![]() 上存在兩點
上存在兩點![]() 使得
使得![]() ,求以
,求以![]() 為直徑的圓面積的取值范圍.
為直徑的圓面積的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)由已知![]() ,列出方程,即可求解點
,列出方程,即可求解點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設點![]() 的坐標為
的坐標為![]() ,當直線
,當直線![]() 斜率不存在時,可得
斜率不存在時,可得![]() ,當直線
,當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() 的方程為
的方程為![]() ,聯立方程組,求解
,聯立方程組,求解![]() ,由此列出不等式組,進而求得
,由此列出不等式組,進而求得![]() ,又由
,又由![]() 為長軸端點時,可求得
為長軸端點時,可求得![]() 的坐標點,求得
的坐標點,求得![]() 的值,即可得到結論.
的值,即可得到結論.
詳解:(1)由已知![]() ,即
,即![]() ,
,
所以![]() ,又三點構成三角形,得
,又三點構成三角形,得![]()
所以點![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]() .
.
(2)設點![]() 的坐標為
的坐標為![]() ,
,
當直線![]() 斜率不存在時,可得
斜率不存在時,可得![]() 分別是短軸的兩端點,得到
分別是短軸的兩端點,得到![]() ,
,
當直線![]() 斜率存在時,設直線
斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,
則由![]() 得
得![]() ①,
①,
聯立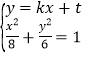 ,得
,得![]() ,
,
由![]() 得
得![]() ,整理得
,整理得![]() .
.
由韋達定理得![]() ,
,![]() ,②
,②
由①②,消去![]() 得
得![]() ,
,
由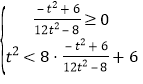 ,解得
,解得![]() ,
,
又因為![]() 為長軸端點
為長軸端點![]() 時,可求得
時,可求得![]() 點
點![]() ,此時
,此時![]() ,
,
綜上,![]() 或
或![]() ,又因為以
,又因為以![]() 為直徑的圓面積
為直徑的圓面積![]() ,
,
所以![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】北京101中學校園內有一個“少年湖”,湖的兩側有一個音樂教室和一個圖書館,如圖,若設音樂教室在A處,圖書館在B處,為測量A,B兩地之間的距離,某同學選定了與A,B不共線的C處,構成△ABC,以下是測量的數據的不同方案:①測量∠A,AC,BC;②測量∠A,∠B,BC;③測量∠C,AC,BC;④測量∠A,∠C,∠B. 其中一定能唯一確定A,B兩地之間的距離的所有方案的序號是_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構對高三學生的記憶力![]() 和判斷力
和判斷力![]() 進行統計分析,得下表數據:
進行統計分析,得下表數據:
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |

(1)請在圖中畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)試根據(2)求出的線性回歸方程,預測記憶力為9的同學的判斷力.
相關公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中, 橢圓
中, 橢圓![]() 的中心在坐標原點
的中心在坐標原點![]() ,其右焦點為
,其右焦點為![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上.
上.

(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓的左、右頂點分別為![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]() 的任意一點,直線
的任意一點,直線![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() ,直線
,直線![]() 交直線
交直線![]() 于
于![]() 點, 求證:
點, 求證:![]() 三點在同一條直線上
三點在同一條直線上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“克拉茨猜想”又稱“![]() 猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數
猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半;如果
是偶數,就將它減半;如果![]() 為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數
為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數![]() 經過6次運算后得到1,則
經過6次運算后得到1,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() 為棱
為棱![]() 的中點,
的中點,![]() 為棱
為棱![]() 上一點,
上一點,![]() .
.

(1)確定![]() 的位置,使得平面
的位置,使得平面![]()
![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)設二面角![]() 的正切值為
的正切值為![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,且
上一點,且![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①函數![]() 是奇函數;
是奇函數;
②將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖像;
的圖像;
③若![]() 是第一象限角且
是第一象限角且![]() ,則
,則![]() ;
;
④![]() 是函數
是函數![]() 的圖像的一條對稱軸;
的圖像的一條對稱軸;
⑤函數![]() 的圖像關于點
的圖像關于點![]() 中心對稱。
中心對稱。
其中,正確的命題序號是______________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com