Question

函數的一段圖象如圖所示．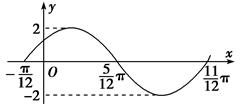

(1)求函數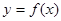的解析式；
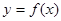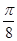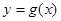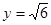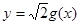(2)將函數的圖象向右平移個單位，得到的圖象，求直線與函數的圖象在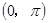內所有交點的坐標．

Answer 1

（1）f(x)＝2sin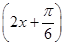（2）交點坐標為.

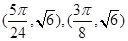解析試題分析：解：(1)由圖知A＝2，T＝π，于是ω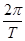＝＝2，      3分
將y＝2sin 2x的圖象向左平移，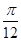
得y＝2sin(2x＋φ)的圖象．
于是φ＝2·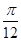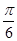＝，                                 4分
∴f(x)＝2sin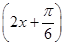.                              5分
(2)依題意得
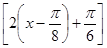g(x)＝2sin=2sin.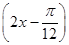
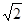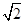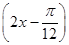故y＝g(x)＝2sin.          7分
由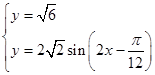
得sin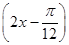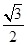＝.                     8分
∴2x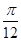－＝＋2kπ或2x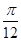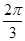－＝＋2kπ(k∈Z)，
∴x＝＋kπ或x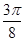＝＋kπ(k∈Z)．      10分
∵x∈(0，π)，
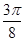∴x＝或x＝.                        11分
∴交點坐標為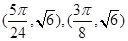.       12分
考點：三角函數圖像以及性質
點評：解決的關鍵是利用整體的思想結合三角函數的性質熟練的求解其解析式以及交點，屬于基礎題。