
���}Ŀ��ijС�^(q��)�����˽�I(y��)����ˮ��r��ԓС�^(q��)�֞�һ�ںͶ��ڣ���ס���_(d��)4000�����F(xi��n)��ͨ�^�S�C(j��)��ӫ@����100��������¾���ˮ�����D���{(di��o)��Y(ji��)�����l��(sh��)�ֲ������l�ʷֲ�ֱ���D��
�ֽM |
|
|
|
|
|
�l��(sh��) | 4 | 8 | 15 | 22 | 25 |
�ֽM |
|
|
|
| |
�l��(sh��) | 14 | 6 | 4 | 2 |
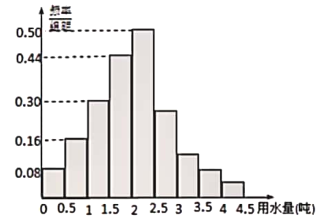
��1����Ӌ(j��)ԓС�^(q��)�¾���ˮ�����^3.8���s�ж��ّ�����2��ͨ�^�l�ʷֲ�ֱ���D����Ӌ(j��)ԓС�^(q��)�����¾���ˮ��ƽ��ֵ����λ��(sh��)��
���𰸡���1��144����2��ƽ����(sh��)2.02����λ��(sh��)2.02
��������
��1������(j��)�l�ʷֲ������ȵõ��¾���ˮ�����^3.8�����l�ʣ��ٳ��Կ��Ñ�����.
��2������(j��)�l�ʷֲ�ֱ���D������ƽ��ֵ��Ӌ(j��)�㹫ʽ��⣬��ǰ�Ă�(g��)С������e��0.49���t��λ��(sh��)�ڵ��傀(g��)С�����У���e��![]() Ӌ(j��)�㼴��.
Ӌ(j��)�㼴��.
��1�����}��֪��
�¾���ˮ�����^3.8�����l�ʼs��![]() ��
��
���Ӌ(j��)ԓС�^(q��)�¾���ˮ�����^3.8���s��![]() ������.
������.
��2�����l�ʷֲ�ֱ���D�е�֪��
ƽ��ֵ![]()
![]() ��
��
��?y��n)�ǰ�Ă�(g��)С������e��0.49���O(sh��)��λ��(sh��)��![]() ��
��
�t![]() ����
����![]() ���������(sh��)2.02.
���������(sh��)2.02.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������Ը�ð�����Q���У������в�������ļ��Ժ�������Ⱦ����һ�N��Ⱦ�ԏ�(qi��ng)�������ٶȿ�ļ���������Ҫͨ�^�՚��е��wĭ�����c��֮�g�Ľ��|���c����Ⱦ��Ʒ�Ľ��|����������ÿ����������ؾ��Ђ��������҇�����ͨ���ʶ��������У��Ϸ��ж��������ļ��ɂ�(g��)���и߷壮��ͯ����(du��)�������ͣ����׃��@���W(xu��)У���ˆT�ܼ��ĵط������ױ���Ⱦ��ij�׃��@��ȥ�괺��ԓ�@������С���Ѱ������g�c�˔�(sh��)�y(t��ng)Ӌ(j��)���õ�����(sh��)��(j��)��
���g�� |
|
|
|
|
|
�����˔�(sh��)�� |
|
|
|
|
|
��1����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw���̣�
�ľ��Իؚw���̣�
��2��Ӌ(j��)��׃��![]() ��
��![]() �����P(gu��n)ϵ��(sh��)
�����P(gu��n)ϵ��(sh��)![]() ��Ӌ(j��)��Y(ji��)�����_��
��Ӌ(j��)��Y(ji��)�����_��![]() �������ش��Ƿ�����J(r��n)��ԓ�׃��@ȥ�괺�ڻ������˔�(sh��)�c���gؓ(f��)���P(gu��n)��(qi��ng)������
�������ش��Ƿ�����J(r��n)��ԓ�׃��@ȥ�괺�ڻ������˔�(sh��)�c���gؓ(f��)���P(gu��n)��(qi��ng)������![]() ���t
���t![]() ��
��![]() ���P(gu��n)�Ժ�(qi��ng)����
���P(gu��n)�Ժ�(qi��ng)����![]() ���t
���t![]() ��
��![]() ���P(gu��n)��һ�㣻��
���P(gu��n)��һ�㣻��![]() ���t
���t![]() ��
��![]() ���P(gu��n)���^������
���P(gu��n)���^������
������(sh��)��(j��)��![]() ��
��
������ʽ�� ��
��
���P(gu��n)ϵ��(sh��)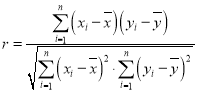 ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�����
�У�����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�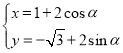 ������
������![]() �酢��(sh��)��
�酢��(sh��)��![]() ��.�ژO����(bi��o)ϵ��������(bi��o)ԭ�c(di��n)
��.�ژO����(bi��o)ϵ��������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �S��ؓ(f��)���S��O�S���У�����
�S��ؓ(f��)���S��O�S���У�����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1��������![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2��������![]() ��ǡ��һ��(g��)�c(di��n)������
��ǡ��һ��(g��)�c(di��n)������![]() �ľ��x��1��������
�ľ��x��1��������![]() ��ֱ������(bi��o)����.
��ֱ������(bi��o)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)������ԭ�c(di��n)�����c(di��n)��![]() �S�ϵęE�A
�S�ϵęE�A![]() �^�c(di��n)
�^�c(di��n)![]() �����x���ʞ�
�����x���ʞ�![]() ��
��![]() ��
��![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ��
��![]() ��һ�c(di��n)��
��һ�c(di��n)��![]() �S��
�S��![]() �İ돽��
�İ돽��![]() ��
��
��1����![]() ��
��![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() �c
�c![]() ����
����![]() ���c(di��n)���c
���c(di��n)���c![]() ����
����![]() ���c(di��n)������
���c(di��n)������![]() �ڵ�һ���ޣ��Ƿ����
�ڵ�һ���ޣ��Ƿ����![]() ʹ
ʹ![]() �������ڣ���
�������ڣ���![]() �ķ��̣��������ڣ��f�����ɣ�
�ķ��̣��������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У���
�У���![]() �����Σ�������
�����Σ�������![]() ���ڵ�ƽ���c
���ڵ�ƽ���c![]() ���ڵ�ƽ�����ֱ��
���ڵ�ƽ�����ֱ��![]() ��
��![]() ��
��![]() ��
��![]() .
.
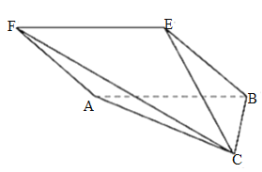
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2���������F![]() �����L��(c��)����L.
�����L��(c��)����L.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У���
�У���![]() �S��ʼ߅���ɂ�(g��)�J��
�S��ʼ߅���ɂ�(g��)�J��![]() �������ĽK߅�քe�c��λ�A�ཻ��A��B���c(di��n)����֪A��B�ęM����(bi��o)�քe��
�������ĽK߅�քe�c��λ�A�ཻ��A��B���c(di��n)����֪A��B�ęM����(bi��o)�քe��![]()

��1����![]() ��ֵ�� ��2����
��ֵ�� ��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ĈD��ăɗl������(du��)�Q�S֮�g�ľ��x��
���ĈD��ăɗl������(du��)�Q�S֮�g�ľ��x��![]() ���҈D����һ��(g��)����c(di��n)��
���҈D����һ��(g��)����c(di��n)��![]() .
.
��1����(sh��)![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ��ֵ��
��ֵ��
��3��������![]() ��
��![]() ���Ѓɂ�(g��)����ȵČ�(sh��)��(sh��)��
���Ѓɂ�(g��)����ȵČ�(sh��)��(sh��)��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)��������
����Ȼ��(du��)��(sh��)�ĵה�(sh��)��������![]() ��
��
������![]() ����
����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
������![]() ���c(di��n)��(g��)��(sh��)��
���c(di��n)��(g��)��(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ������
�S�������S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��ֱ��
��ֱ��![]() �c
�c![]() �S�����c(di��n)
�S�����c(di��n)![]() ���c����
���c����![]() ���ڃ��c(di��n)
���ڃ��c(di��n)![]() ��
��![]() ��
��
��1��������![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2����![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com