
【題目】如圖,直線AB經過⊙O上的點C,并且OA=OB,CA=CB,⊙O交直線OB于E、D,連接EC、CD. 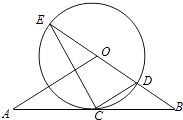
(1)求證:直線AB是⊙O的切線;
(2)若tan∠CED= ![]() ,⊙O的半徑為3,求OA的長.
,⊙O的半徑為3,求OA的長.
【答案】
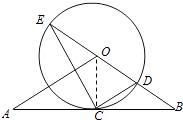
(1)解:如圖,連接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∴AB是⊙O的切線
(2)解:∵BC是圓O切線,且BE是圓O割線,
∴BC2=BDBE,
∵tan∠CED= ![]() ,∴
,∴ ![]() .
.
∵△BCD∽△BEC,∴ ![]() ,
,
設BD=x,BC=2x.又BC2=BDBE,∴(2x)2=x(x+6),
解得x1=0,x2=2,∵BD=x>0,∴BD=2,∴OA=OB=BD+OD=3+2=5
【解析】(1)要想證AB是⊙O的切線,只要連接OC,求證∠ACO=90°即可;(2)先由三角形判定定理可知,△BCD∽△BEC,得BD與BC的比例關系,最后由切割線定理列出方程求出OA的長.
【考點精析】解答此題的關鍵在于理解直線的參數方程的相關知識,掌握經過點![]() ,傾斜角為
,傾斜角為![]() 的直線
的直線![]() 的參數方程可表示為
的參數方程可表示為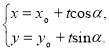 (
(![]() 為參數).
為參數).


科目:高中數學 來源: 題型:
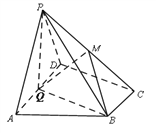
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q為AD的中點,M是棱
底面ABCD,Q為AD的中點,M是棱![]() 上的點,
上的點, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() ;
;
(Ⅱ)若二面角![]() 的大小為
的大小為![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的左右頂點分別為A(﹣2,0),B(2,0),橢圓上除A、B外的任一點C滿足kACkBC=﹣ ![]() .
. 
(1)求橢圓C的標準方程;
(2)過點P(4,0)任作一條直線l與橢圓C交于不同的兩點M,N,在x軸上是否存在點Q,使得∠PQM+∠PQN=180°?若存在,求出點Q的坐標;若不存在,請說明現由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的另一個焦點是
的另一個焦點是![]() ,且
,且![]() .
.
(1) 求橢圓![]() 的方程;
的方程;
(2) 直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的內切圓面積的最大值.
的內切圓面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com