
【題目】已知常數a>0,函數f(x)=ln(1+ax)﹣ ![]() .
.
(Ⅰ)討論f(x)在區間(0,+∞)上的單調性;
(Ⅱ)若f(x)存在兩個極值點x1 , x2 , 且f(x1)+f(x2)>0,求a的取值范圍.
【答案】解:(Ⅰ)∵f(x)=ln(1+ax)﹣ ![]() . ∴f′(x)=
. ∴f′(x)= ![]() =
= 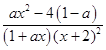 ,
,
∵(1+ax)(x+2)2>0,∴當1﹣a≤0時,即a≥1時,f′(x)≥0恒成立,則函數f(x)在(0,+∞)單調遞增,
當0<a≤1時,由f′(x)=0得x=± 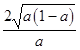 ,則函數f(x)在(0,
,則函數f(x)在(0, 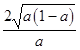 )單調遞減,在(
)單調遞減,在( 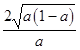 ,+∞)單調遞增.
,+∞)單調遞增.
(Ⅱ)由(Ⅰ)知,當a≥1時,f′(x)≥0,此時f(x)不存在極值點.
因此要使f(x)存在兩個極值點x1 , x2 , 則必有0<a<1,又f(x)的極值點值可能是x1= 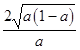 ,x2=﹣
,x2=﹣ 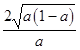 ,
,
且由f(x)的定義域可知x>﹣ ![]() 且x≠﹣2,
且x≠﹣2,
∴﹣ 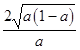 >﹣
>﹣ ![]() 且﹣
且﹣ 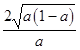 ≠﹣2,解得a≠
≠﹣2,解得a≠ ![]() ,則x1 , x2分別為函數f(x)的極小值點和極大值點,
,則x1 , x2分別為函數f(x)的極小值點和極大值點,
∴f(x1)+f(x2)=ln[1+ax1]﹣ ![]() +ln(1+ax2)﹣
+ln(1+ax2)﹣ ![]() =ln[1+a(x1+x2)+a2x1x2]﹣
=ln[1+a(x1+x2)+a2x1x2]﹣ 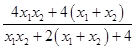
=ln(2a﹣1)2﹣ ![]() =ln(2a﹣1)2+
=ln(2a﹣1)2+ ![]() ﹣2.
﹣2.
令2a﹣1=x,由0<a<1且a≠ ![]() 得,
得,
當0<a< ![]() 時,﹣1<x<0;當
時,﹣1<x<0;當 ![]() <a<1時,0<x<1.
<a<1時,0<x<1.
令g(x)=lnx2+ ![]() ﹣2.
﹣2.
(i)當﹣1<x<0時,g(x)=2ln(﹣x)+ ![]() ﹣2,∴g′(x)=
﹣2,∴g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
故g(x)在(﹣1,0)上單調遞減,g(x)<g(﹣1)=﹣4<0,
∴當0<a< ![]() 時,f(x1)+f(x2)<0;
時,f(x1)+f(x2)<0;
(ii)當0<x<1.g(x)=2lnx+ ![]() ﹣2,g′(x)=
﹣2,g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
故g(x)在(0,1)上單調遞減,g(x)>g(1)=0,
∴當 ![]() <a<1時,f(x1)+f(x2)>0;
<a<1時,f(x1)+f(x2)>0;
綜上所述,a的取值范圍是( ![]() ,1)
,1)
【解析】(Ⅰ)利用導數判斷函數的單調性,注意對a分類討論;(Ⅱ)利用導數判斷函數的極值,注意a的討論及利用換元法轉化為求函數最值問題解決.
【考點精析】利用利用導數研究函數的單調性和函數的極值對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;極值反映的是函數在某一點附近的大小情況.
在這個區間單調遞減;極值反映的是函數在某一點附近的大小情況.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源: 題型:
【題目】設f(x)=|ax﹣1|.
(Ⅰ)若f(x)≤2的解集為[﹣6,2],求實數a的值;
(Ⅱ)當a=2時,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤7﹣3m成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an},{bn}滿足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4 及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn} 的通項公式,并證明你的結論;
(Ⅲ)證明:對所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,在陽馬P﹣ABCD中,側棱PD⊥底面ABCD,且PD=CD,過棱PC的中點E,作EF⊥PB交PB于點F,連接DE,DF,BD,BE. 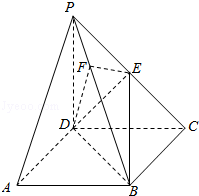
(1)證明:PB⊥平面DEF.試判斷四面體DBEF是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(2)若面DEF與面ABCD所成二面角的大小為 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax(a>0,a≠1)在區間[﹣1,2]上的最大值為8,最小值為m.若函數g(x)=(3﹣10m) ![]() 是單調增函數,則a= .
是單調增函數,則a= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱柱ABC﹣A1B1C1的側棱與底面邊長都相等,A1在底面ABC上的射影D為BC的中點,則異面直線AB與CC1所成的角的余弦值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的各項都是正數,且對任意n∈N*都有a13+a23+a33+…+an3=Sn2 , 其中Sn為數列{an}的前n和.
(1)求證:an2=2Sn﹣an;
(2)求數列{an}的通項公式
(3)設bn=3n+(﹣1)n﹣1λ2 ![]() (λ為非零整數,n∈N*)試確定λ的值,使得對任意n∈N*,都有bn+1>bn成立.
(λ為非零整數,n∈N*)試確定λ的值,使得對任意n∈N*,都有bn+1>bn成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com