
【題目】求函數f(x)=sinx+cosx+sinxcosx的值域________.
【答案】[﹣1, ![]() +
+ ![]() ]
]
【解析】解:令t=sinx+cosx= ![]() sin(x+
sin(x+ ![]() ),
),
則﹣ ![]() ≤t≤
≤t≤ ![]() ,t2=1+2sinxcosx,
,t2=1+2sinxcosx,
則sinxcosx= ![]() ,
,
則f(x)=sinx+cosx+sinxcosx
=t+ ![]() =
= ![]() (t2+2t﹣1)
(t2+2t﹣1)
= ![]() (t+1)2﹣1;
(t+1)2﹣1;
∵﹣ ![]() ≤t≤
≤t≤ ![]() ,
,
∴﹣1≤ ![]() (t+1)2﹣1≤
(t+1)2﹣1≤ ![]() +
+ ![]() ;
;
故函數f(x)=sinx+cosx+sinxcosx的值域為[﹣1, ![]() +
+ ![]() ].
].
【考點精析】掌握函數的值域和三角函數的最值是解答本題的根本,需要知道求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的;函數![]() ,當
,當![]() 時,取得最小值為
時,取得最小值為![]() ;當
;當![]() 時,取得最大值為
時,取得最大值為![]() ,則
,則![]() ,
,![]() ,
,![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)如圖,四棱錐![]() 的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,連結
的中點,連結![]() .求證:
.求證:
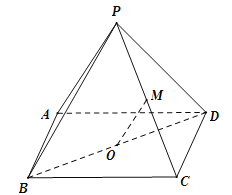
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】航空測量組的飛機航線和山頂在同一鉛直平面內,已知飛機的高度為海拔10000m,速度為180km(千米)/h(小時),飛機先看到山頂的俯角為15°,經過420s(秒)后又看到山頂的俯角為45°,求山頂的海拔高度(取 ![]() ,
, ![]() ).
). 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面內的三個向量,其中
是同一平面內的三個向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐標;
的坐標;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 與2
與2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 與
與 ![]() 的夾角θ.
的夾角θ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個水輪的半徑為4m,水輪圓心O距離水面2m,已知水輪每分鐘轉動5圈,如果當水輪上點P從水中浮現時(圖中點p0)開始計算時間. 
(1)將點p距離水面的高度z(m)表示為時間t(s)的函數;
(2)點p第一次到達最高點大約需要多少時間?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中,D為AB的中點.
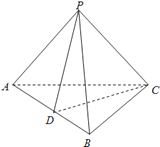
(1)與BC平行的平面PDE交AC于點E,判斷點E在AC上的位置并說明理由如下:
(2)若PA=PB,且△PCD為銳角三角形,又平面PCD⊥平面ABC,求證:AB⊥PC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,當∠xOy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)時,定義平面坐標系xOy為α﹣仿射坐標系.在α﹣仿射坐標系中,任意一點P的斜坐標這樣定義:
,π)時,定義平面坐標系xOy為α﹣仿射坐標系.在α﹣仿射坐標系中,任意一點P的斜坐標這樣定義: ![]() 、
、 ![]() 分別為與x軸、y軸正向相同的單位向量,若
分別為與x軸、y軸正向相同的單位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,則記為
,則記為 ![]() =(x,y).現給出以下說法:
=(x,y).現給出以下說法:
①在α﹣仿射坐標系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,則t=6;
,則t=6;
②在α﹣仿射坐標系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),則
),則 ![]()
![]() =0;
=0;
③在60°﹣仿射坐標系中,若P(2,﹣1),則| ![]() |=
|= ![]() ;
;
其中說法正確的有 . (填出所有說法正確的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P-ABC中,D為AB的中點。

(1)與BC平行的平面PDE交AC于點E,判斷點E在AC上的位置并說明理由如下:
(2)若PA=PB,且△PCD為銳角三角形,又平面PCD⊥平面ABC,求證:AB⊥PC。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知PA垂直于矩形ABCD所在的平面,M,N分別是AB,PC的中點,若∠PDA=45°, 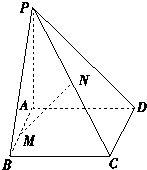
(1)求證:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD滿足什么條件時,有PC⊥BD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com