
【題目】已知![]() .
.
(Ⅰ)當![]() 時,若關于
時,若關于![]() 的方程
的方程![]() 有且只有兩個不同的實根,求實數
有且只有兩個不同的實根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)對任意![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(Ⅰ) ![]() ;(Ⅱ)1.
;(Ⅱ)1.
【解析】試題分析:
(Ⅰ) 當![]() 時,
時, ![]() ,結合圖象可得若方程
,結合圖象可得若方程![]() 有且只有兩個不同的實根,只需
有且只有兩個不同的實根,只需![]() 即可.(Ⅱ)由題意得只需滿足
即可.(Ⅱ)由題意得只需滿足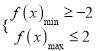 即可,根據函數
即可,根據函數![]() 圖象的對稱軸
圖象的對稱軸![]() 與區間
與區間![]() 的關系及拋物線的開口方向求得函數的最值,然后解不等式可得所求.
的關系及拋物線的開口方向求得函數的最值,然后解不等式可得所求.
試題解析:
(Ⅰ)當![]() 時,
時, ![]() ,
,
∵關于![]() 的方程
的方程![]() 有且只有兩個不同的實根,
有且只有兩個不同的實根,
∴![]() ,
,
∴![]() .
.
∴實數![]() 的取值范圍為
的取值范圍為![]() .
.
(Ⅱ)①當![]()
![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
∵不等式![]() 恒成立,
恒成立,
∴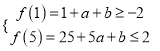 ,可得
,可得![]() ,
,
∴![]()
解得![]() ,與
,與![]() 矛盾,不合題意.
矛盾,不合題意.
②當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
∵不等式![]() 恒成立,
恒成立,
∴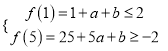 ,可得
,可得![]()
∴![]()
解得![]() ,這與
,這與![]() 矛盾,不合題意.
矛盾,不合題意.
③當![]() ,即
,即![]() 時,
時,
∵不等式![]() 恒成立,
恒成立,
∴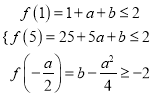 ,整理得
,整理得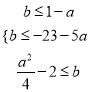 ,
,
即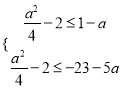 ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() .
.
當![]() 時,則
時,則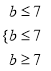 ,故
,故![]() .
.
∴![]() .
.
綜上可得![]() .
.


科目:高中數學 來源: 題型:
【題目】“奶茶妹妹”對某時間段的奶茶銷售量及其價格進行調查,統計出售價x元和銷售量y杯之間的一組數據如下表所示:
價格x | 5 | 5.5 | 6.5 | 7 |
銷售量y | 12 | 10 | 6 | 4 |
通過分析,發現銷售量y對奶茶的價格x具有線性相關關系.
(Ⅰ)求銷售量y對奶茶的價格x的回歸直線方程;
(Ⅱ)欲使銷售量為13杯,則價格應定為多少?
注:在回歸直線y= ![]() 中,
中,  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程.
的一元二次方程. ![]() .
.
(1)若![]() 是從0、1、2、3四個數中任取的一個數,
是從0、1、2、3四個數中任取的一個數, ![]() 是從0、1、2三個數中任取的一個數,求上述方程有實數根的概率;
是從0、1、2三個數中任取的一個數,求上述方程有實數根的概率;
(2)若![]() 是從區間
是從區間![]() 任取的一個數,
任取的一個數, ![]() 是從區間
是從區間![]() 任取的一個數,求上述方程有實數根的概率.
任取的一個數,求上述方程有實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈R,x+ ![]() ≥2;命題q:x0∈
≥2;命題q:x0∈ ![]() ,使sin x0+cos x0=
,使sin x0+cos x0= ![]() ,
,
則下列命題中為真命題的是( )
A.( ![]() p)∧q
p)∧q
B.p∧( ![]() q)
q)
C.( ![]() p)∧(
p)∧( ![]() q)
q)
D.p∧q
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 與四棱錐
與四棱錐![]() 的組合體中,已知
的組合體中,已知![]() 平面
平面![]() ,四邊形
,四邊形![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,設
,設![]() 是線段
是線段![]() 中點.
中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com