【題目】設關于
的一元二次方程. 
.
(1)若
是從0、1、2、3四個數中任取的一個數， 
是從0、1、2三個數中任取的一個數，求上述方程有實數根的概率；
(2)若
是從區間
任取的一個數， 
是從區間
任取的一個數，求上述方程有實數根的概率.
【答案】(1) 
(2) 
【解析】試題分析：（1）由一元二次方程的判別式大于等于0得到方程
有實數根的充要條件為a≥b，用列舉法求出a從0，1，2，3四個數中任取的一個數，b從0，1，2三個數中任取的一個數的所有基本事件個數，查出滿足a≥b的事件數，然后直接利用古典概型的概率計算公式求解；（2）由題意求出點（a，b）所構成的矩形面積，再由線性規劃知識求出滿足a≥b的區域面積，由測度比是面積比求概率.
試題解析：
設事件
為“方程
有實根”，
方程
有實根的充要條件為
.
(1)基本事件共 12 個：
，
其中括號第一個數表示
的取值袁第二個數表示
的取值.
事件
中包含 9 個基本事件， 
，事件
發生的概率為； 
；
(2)試驗的全部結束所構成的區域為
，
構成事件
的區域為
，
所以所求的概率為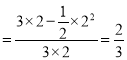
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知在四棱錐P﹣ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E，F分別是線段AB，BC的中點．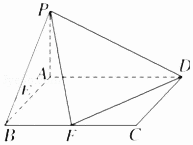 
（1）證明：PF⊥FD；
（2）若PA=1，求點E到平面PFD的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
有如下性質：如果常數
，那么該函數
上是減函數，在
上是增函數．
（1）用函數單調性定義來證明
上的單調性；
（2）已知
， 
，求函數
的值域；
（3）對于（2）中的函數
和函數
，若對任意
，總存在
，使得
成立，求實數
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在R上的奇函數f（x）滿足f（x﹣2）=f（x+2），且當x∈[﹣2，0]時，f（x）=3x﹣1，則f（9）=（ ）
A.﹣2
B.2
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
與四棱錐
的組合體中，已知
平面
，四邊形
是平行四邊形， 
， 
， 
， 
，設
是線段
中點.
(1)求證： 
平面
；
(2)證明：平面
平面
；
(3)求四棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）＝－3x2＋a（6－a）x＋6.
（1）解關于a的不等式f（1）>0；
（2）若不等式f（x）>b的解集為（－1,3），求實數a，b的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
