
已知
(1)求 的極值,
的極值,
并證明:若 有
有 ;
;
(2)設 ,且
,且 ,
, ,
,
證明: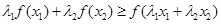 ,
,
若 ,由上述結論猜想一個一般性結論(不需要證明);
,由上述結論猜想一個一般性結論(不需要證明);
(3)證明:若 ,則
,則
(1)0,利用作差法即可證明;(2)利用綜合法即可證明,猜想:若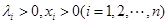 ,且
,且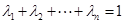 時有
時有
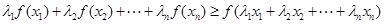 ;(3)利用第(2)問的結論及對數的運算證明即可
;(3)利用第(2)問的結論及對數的運算證明即可
【解析】
試題分析:(1)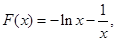 則
則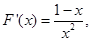
當x∈(0,1)時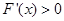 ,x∈(1,+∞)時
,x∈(1,+∞)時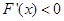 ,
,
∴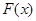 在(0,1)遞增,在(1,+∞)遞減,
在(0,1)遞增,在(1,+∞)遞減,
,∴當x=1時,F(x)有極大值為0,且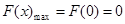 2分
2分
∴當 時
時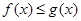 恒成立,即
恒成立,即 時
時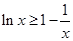 恒成立。
恒成立。
∴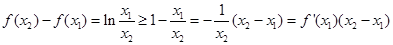 4分
4分
(2)證明:設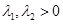 ,且
,且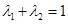 ,令
,令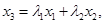 ,則
,則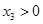 ,且
,且
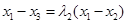 ,
,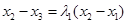 ,
,
由(1)可知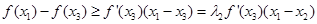 ①
①
 ②
②
①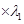 +②
+②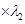 ,得
,得
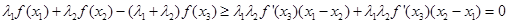
∴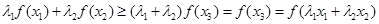 8分
8分
猜想:若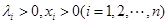 ,且
,且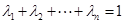 時有
時有
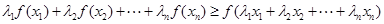 9分
9分
(3)證明:令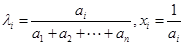
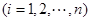
由猜想結論得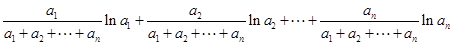
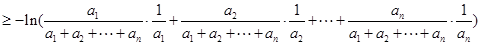
=
∴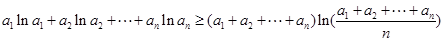 ,
,
即有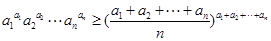 。 14分
。 14分
考點:本題考查了導數的運用
點評:導數本身是個解決問題的工具,是高考必考內容之一,高考往往結合函數甚至是實際問題考查導數的應用,求單調、最值、完成證明等,請注意歸納常規方法和常見注意點


科目:高中數學 來源:2012-2013學年湖北省黃岡市高三下學期6月適應性考試理科數學試卷(解析版) 題型:解答題
已知 .
.
(1)求 的極值,并證明:若
的極值,并證明:若 有
有 ;
;
(2)設 ,且
,且 ,
, ,證明:
,證明: ,
,
若 ,由上述結論猜想一個一般性結論(不需要證明);
,由上述結論猜想一個一般性結論(不需要證明);
(3)證明:若 ,則
,則 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com