
【題目】(1)已知圓![]() 的圓心是直線
的圓心是直線![]() 與
與![]() 軸的交點(diǎn),且與直線
軸的交點(diǎn),且與直線![]() 相切,求圓
相切,求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知圓![]() ,直線
,直線![]() 過點(diǎn)
過點(diǎn)![]() 與圓
與圓![]() 相交于
相交于![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)求出直線x﹣y+1=0與x軸的交點(diǎn)即為圓心C坐標(biāo),求出點(diǎn)C到直線x+y+3=0的距離
即為圓的半徑,寫出圓的標(biāo)準(zhǔn)方程即可;(2) 由題意畫出圖象,由弦長(zhǎng)公式求出圓心到直線
l的距離,對(duì)直線l的斜率分類討論,根據(jù)點(diǎn)到直線的距離公式求出直線的斜率,即可求出
直線l的方程.
(1)對(duì)于直線x﹣y+1=0,令y=0,得到x=﹣1,即圓心C(﹣1,0),
∵圓心C(﹣1,0)到直線x+y+3=0的距離d=![]() =
=![]() ,
,
∴圓C半徑r=![]() ,
,
則圓C方程為(x+1)2+y2=2;
(2) 由題意畫出圖象,如圖所示:
過圓心C作CM⊥PQ,則|MP|=|MQ|=![]() |PQ|=
|PQ|=![]() ,
,
由圓C的方程得到圓心C坐標(biāo)(0,3),半徑r=2,
在Rt△CPM中,根據(jù)勾股定理得:CM=1,
即圓心到直線的距離為1,
①當(dāng)直線l的斜率不存在時(shí),顯然直線x=﹣1滿足題意;
②當(dāng)直線l的斜率存在時(shí),設(shè)直線l的斜率為k,
又過A(﹣1,0),則直線l的方程為y=k(x+1),
即kx﹣y+k=0,
∴圓心到直線l的距離d=![]() =1,解得k=
=1,解得k=![]() ,
,
∴直線l的方程為4x﹣3y+4=0,
綜上,滿足題意的直線l為x=﹣1或4x﹣3y+4=0.
故答案為:x=﹣1或4x﹣3y+4=0.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)是世界上嚴(yán)重缺水的國(guó)家,某市政府為了鼓勵(lì)居民節(jié)約用水,計(jì)劃調(diào)整居民生活用水收費(fèi)方案,擬確定一個(gè)合理的月用水量標(biāo)準(zhǔn)![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過![]() 的部分按平價(jià)收費(fèi),超出
的部分按平價(jià)收費(fèi),超出![]() 的部分按議價(jià)收費(fèi)。為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照
的部分按議價(jià)收費(fèi)。為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照![]() ,
,![]() …,
…,![]() 分成9組,制成了如圖所示的頻率分布直方圖。
分成9組,制成了如圖所示的頻率分布直方圖。

(1)求直方圖中![]() 的值;
的值;
(2)設(shè)該市有60萬(wàn)居民,估計(jì)全市居民中月均用水量不低于3噸的人數(shù),并說(shuō)明理由;
(3)若該市政府希望使82%的居民每月的用水量不超過標(biāo)準(zhǔn)![]() (噸),估計(jì)
(噸),估計(jì)![]() 的值,并說(shuō)明理由。
的值,并說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an}滿足a1=0,an+1=an+2 ![]() +1
+1
(1)求證數(shù)列{ ![]() }是等差數(shù)列,并求出an的通項(xiàng)公式;
}是等差數(shù)列,并求出an的通項(xiàng)公式;
(2)若bn= ![]() ,求數(shù)列{b}的前n項(xiàng)的和Tn .
,求數(shù)列{b}的前n項(xiàng)的和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓C的中心在原點(diǎn),焦點(diǎn)在x軸上,它的一個(gè)頂點(diǎn)恰好是拋物線y= ![]() x2的焦點(diǎn),離心率等于
x2的焦點(diǎn),離心率等于 ![]() .
.
(1)求橢圓C的方程;
(2)過橢圓C的右焦點(diǎn)F作直線l交橢圓C于A、B兩點(diǎn),交y軸于M點(diǎn),若 ![]() =λ1
=λ1 ![]() ,
, ![]() ,求證:λ1+λ2為定值.
,求證:λ1+λ2為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() , 傾斜角為
, 傾斜角為![]() 的直線
的直線![]() 經(jīng)過橢圓
經(jīng)過橢圓![]() 的右焦點(diǎn)且與圓
的右焦點(diǎn)且與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相切于點(diǎn)
相切于點(diǎn)![]() , 且交橢圓
, 且交橢圓![]() 于
于![]() 兩點(diǎn),射線
兩點(diǎn),射線![]() 于橢圓
于橢圓![]() 交于點(diǎn)
交于點(diǎn)![]() ,設(shè)
,設(shè)![]() 的面積與
的面積與![]() 的面積分別為
的面積分別為![]() .
.
①求![]() 的最大值; ②當(dāng)
的最大值; ②當(dāng)![]() 取得最大值時(shí),求
取得最大值時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】進(jìn)入冬季以來(lái),我國(guó)北方地區(qū)的霧霾天氣持續(xù)出現(xiàn),極大的影響了人們的健康和出行,我市環(huán)保局對(duì)該市2015年進(jìn)行為期一年的空氣質(zhì)量監(jiān)測(cè),得到每天的空氣質(zhì)量指數(shù),從中隨機(jī)抽取50個(gè)作為樣本進(jìn)行分析報(bào)告,樣本數(shù)據(jù)分組區(qū)間為(5,15],(15,25],(25,35],(35,45],由此得到樣本的空氣質(zhì)量指數(shù)頻率分布直方圖,如圖.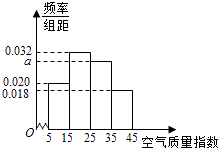
(1)求a的值;
(2)如果空氣質(zhì)量指數(shù)不超過15,就認(rèn)定空氣質(zhì)量為“特優(yōu)等級(jí)”,則從今年的監(jiān)測(cè)數(shù)據(jù)中隨機(jī)抽取3天的數(shù)值,其中達(dá)到“特優(yōu)等級(jí)”的天數(shù)為X.求X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】第31屆夏季奧林匹克運(yùn)動(dòng)會(huì)于2016年8月5日至8月21日在巴西里約熱內(nèi)盧舉行.如表是近五屆奧運(yùn)會(huì)中國(guó)代表團(tuán)和俄羅斯代表團(tuán)獲得的金牌數(shù)的統(tǒng)計(jì)數(shù)據(jù)(單位:枚).
第30屆倫敦 | 第29屆北京 | 第28屆雅典 | 第27屆悉尼 | 第26屆亞特蘭大 | |
中國(guó) | 38 | 51 | 32 | 28 | 16 |
俄羅斯 | 24 | 23 | 27 | 32 | 26 |
(1)根據(jù)表格中兩組數(shù)據(jù)在答題卡上完成近五屆奧運(yùn)會(huì)兩國(guó)代表團(tuán)獲得的金牌數(shù)的莖葉圖,并通過莖葉圖比較兩國(guó)代表團(tuán)獲得的金牌數(shù)的平均值及分散程度(不要求計(jì)算出具體數(shù)值,給出結(jié)論即可);
(2)如表是近五屆奧運(yùn)會(huì)中國(guó)代表團(tuán)獲得的金牌數(shù)之和![]() (從第26屆算起,不包括之前已獲得的金牌數(shù))隨時(shí)間
(從第26屆算起,不包括之前已獲得的金牌數(shù))隨時(shí)間![]() 變化的數(shù)據(jù):
變化的數(shù)據(jù):
時(shí)間 | 26 | 27 | 28 | 29 | 30 |
金牌數(shù)之和 | 16 | 44 | 76 | 127 | 165 |
作出散點(diǎn)圖如圖:

由圖可以看出,金牌數(shù)之和![]() 與時(shí)間
與時(shí)間![]() 之間存在線性相關(guān)關(guān)系,請(qǐng)求出
之間存在線性相關(guān)關(guān)系,請(qǐng)求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,并預(yù)測(cè)從第26屆到第32屆奧運(yùn)會(huì)時(shí)中國(guó)代表團(tuán)獲得的金牌數(shù)之和為多少?
的線性回歸方程,并預(yù)測(cè)從第26屆到第32屆奧運(yùn)會(huì)時(shí)中國(guó)代表團(tuán)獲得的金牌數(shù)之和為多少?
附:對(duì)于一組數(shù)據(jù)![]() ,
, ![]() ,…,
,…, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為: ,
,
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an}中, ![]() ,若利用下面程序框圖計(jì)算該數(shù)列的第2016項(xiàng),則判斷框內(nèi)的條件是( )
,若利用下面程序框圖計(jì)算該數(shù)列的第2016項(xiàng),則判斷框內(nèi)的條件是( ) 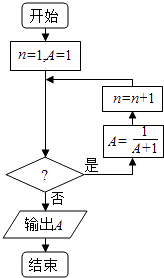
A.n≤2014
B.n≤2016
C.n≤2015
D.n≤2017
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com