
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為矩形,PA⊥平面ABCD,AP=1,AD=2,E為線段PD上一點,記 ![]() =λ. 當λ=
=λ. 當λ= ![]() 時,二面角D﹣AE﹣C的平面角的余弦值為
時,二面角D﹣AE﹣C的平面角的余弦值為 ![]() .
. 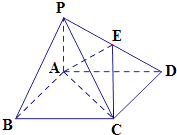
(1)求AB的長;
(2)當 ![]() 時,求異面直線BP與直線CE所成角的余弦值.
時,求異面直線BP與直線CE所成角的余弦值.
【答案】
(1)解:∵PA⊥平面ABCD,ABCD為矩形,∴AB,AD,AP兩兩垂直.
如圖,以A為坐標原點,AB,AD,AP的方向為x軸、y軸、z軸的正方向,
建立空間直角坐標系Axyz,
則D(0,2,0),E(0,1, ![]() ),
), ![]() =(0,1,
=(0,1, ![]() ).
).
設B(m,0,0)(m>0),則C(m,2,0), ![]() =(m,2,0).
=(m,2,0).
設 ![]() =(x,y,z)為平面ACE的法向量,
=(x,y,z)為平面ACE的法向量,
則 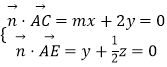 ,取z=2,得
,取z=2,得 ![]() =(
=( ![]() ,﹣1,2).
,﹣1,2).
又 ![]() =(1,0,0)為平面DAE的法向量,
=(1,0,0)為平面DAE的法向量,
∵二面角D﹣AE﹣C的平面角的余弦值為 ![]() ,
,
∴由題設知|cos< ![]() >|=
>|= ![]() ,即
,即 ![]() ,
,
解得m=1,即AB=1
(2)解: ![]() ,
,
∴ ![]() ,
,
![]() ,
, ![]()
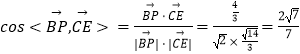 ,
,
∴異面直線BP與直線CE所成角的余弦值為 ![]() .
.
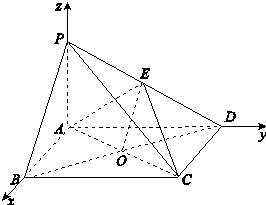
【解析】(1)以A為坐標原點,AB,AD,AP的方向為x軸、y軸、z軸的正方向,建立空間直角坐標系Axyz,利用向量法能求出AB.(2)分別求出 ![]() ,
, ![]() ,利用向量法能求出異面直線BP與直線CE所成角的余弦值.
,利用向量法能求出異面直線BP與直線CE所成角的余弦值.
【考點精析】根據(jù)題目的已知條件,利用異面直線及其所成的角的相關知識可以得到問題的答案,需要掌握異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點,作另一條的平行線;2、補形法:把空間圖形補成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發(fā)現(xiàn)兩條異面直線間的關系.


科目:高中數(shù)學 來源: 題型:
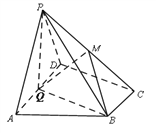
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q為AD的中點,M是棱
底面ABCD,Q為AD的中點,M是棱![]() 上的點,
上的點, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() ;
;
(Ⅱ)若二面角![]() 的大小為
的大小為![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,底面△ABC為等腰直角三角形,∠B=90°,D為棱BB1上一點,且平面DA1C⊥平面AA1C1C. 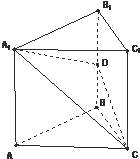
(1)求證:D點為棱BB1的中點;
(2)判斷四棱錐A1﹣B1C1CD和C﹣A1ABD的體積是否相等,并證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的另一個焦點是
的另一個焦點是![]() ,且
,且![]() .
.
(1) 求橢圓![]() 的方程;
的方程;
(2) 直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的內切圓面積的最大值.
的內切圓面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列{an}滿足a1+3a2+32a3+…+3n﹣1an= ![]() (n∈N*).
(n∈N*).
(1)求數(shù)列{an}的通項公式;
(2)設bn= ![]() ,求數(shù)列{bn}的前n項和Sn .
,求數(shù)列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校高三(1)班的一次數(shù)學測試成績的莖葉圖和頻舉分布直方圖都受到不同程度的破壞,可見部分
如下.


(1)求全班人數(shù)及分數(shù)在![]() 內的頻數(shù);
內的頻數(shù);
(2)估計該班的平均分數(shù),并計算頻率分布直方圖中![]() 的矩形的高;
的矩形的高;
(3)若要從分數(shù)在![]() 內的試卷中任取兩份分析學生的失分情況,在抽取的試卷中,求至少有一份分數(shù)在
內的試卷中任取兩份分析學生的失分情況,在抽取的試卷中,求至少有一份分數(shù)在![]() 內的概率.
內的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com