
【題目】![]() 是雙曲線
是雙曲線![]() 的左右焦點,過
的左右焦點,過![]() 且斜率為1的直線與兩條漸近線分別交于
且斜率為1的直線與兩條漸近線分別交于![]() 兩點,若
兩點,若![]() ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】設直線方程為![]() ,與漸近線方程
,與漸近線方程![]() 聯立方程組解得
聯立方程組解得![]() 因為
因為![]() ,所以
,所以![]()
![]() ,選B.
,選B.
點睛:解決橢圓和雙曲線的離心率的求值及范圍問題其關鍵就是確立一個關于![]() 的方程或不等式,再根據
的方程或不等式,再根據![]() 的關系消掉
的關系消掉![]() 得到
得到![]() 的關系式,而建立關于
的關系式,而建立關于![]() 的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
【題型】單選題
【結束】
10
【題目】設![]() 是兩條不同的直線,
是兩條不同的直線, ![]() 是兩個不同的平面,則下列命題中正確的是( )
是兩個不同的平面,則下列命題中正確的是( )
A. 若![]() ,
, ![]() ,則
,則![]()
B. 若![]() ,
, ![]() ,則
,則![]()
C. 若![]() ,
, ![]() ,
, ![]() ,則
,則![]()
D. 若![]() ,且
,且![]() ,點
,點![]() ,直線
,直線![]() ,則
,則![]()
科目:高中數學 來源: 題型:
【題目】(2016·山東卷)已知數列{an}的前n項和Sn=3n2+8n,{bn}是等差數列,且an=bn+bn+1.
(1)求數列{bn}的通項公式;
(2)令cn=![]() ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角坐標系![]() 中,圓
中,圓![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,過點
,過點![]() 的直線
的直線![]() ,
,![]() 分別與圓
分別與圓![]() 交于
交于![]() 兩點.
兩點.
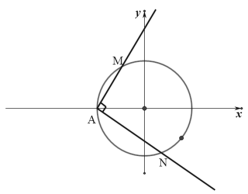
(1)過點![]()
![]() 作圓
作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,求
,求![]() ;
;
(2)若![]() ,求證:直線
,求證:直線![]() 過定點
過定點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系![]() 中,直線
中,直線![]() 過點
過點![]() ,且傾斜角為
,且傾斜角為![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,半徑為4的圓
軸的正半軸為極軸,建立極坐標系,半徑為4的圓![]() 的圓心的極坐標為
的圓心的極坐標為![]() 。
。
(Ⅰ)寫出直線![]() 的參數方程和圓
的參數方程和圓![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)試判定直線![]() 和圓
和圓![]() 的位置關系.
的位置關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com