
【題目】已知雙曲線![]() 的右頂點為
的右頂點為![]() , 以
, 以![]() 為圓心的圓與雙曲線
為圓心的圓與雙曲線![]() 的某一條漸近線交于兩點
的某一條漸近線交于兩點![]() .若
.若![]() ,且
,且![]() (其中
(其中![]() 為原點),則雙曲線
為原點),則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
設雙曲線的一條漸近線方程為![]() x,A(a,0),P(m,
x,A(a,0),P(m,![]() ),(m>0),由向量共線的坐標表示,可得Q的坐標,求得弦長|PQ|,運用中點坐標公式,可得PQ的中點坐標,由兩直線垂直的條件:斜率之積為﹣1,可得m
),(m>0),由向量共線的坐標表示,可得Q的坐標,求得弦長|PQ|,運用中點坐標公式,可得PQ的中點坐標,由兩直線垂直的條件:斜率之積為﹣1,可得m![]() ,r
,r![]() ,運用圓的弦長公式計算即可得到a,b的關系,再由離心率公式計算即可得到所求值.
,運用圓的弦長公式計算即可得到a,b的關系,再由離心率公式計算即可得到所求值.
解:設雙曲線的一條漸近線方程
為y![]() x,A(a,0),
x,A(a,0),
P(m,![]() ),(m>0),
),(m>0),
由![]() 3
3![]() ,可得Q(3m,
,可得Q(3m,![]() ),
),
圓的半徑為r=|PQ|![]() 2m
2m![]() ,
,
PQ的中點為H(2m,![]() ),
),
由AH⊥PQ,可得![]() ,
,
解得m![]() ,r
,r![]() .
.
A到漸近線的距離為d![]() ,
,
則|PQ|=2![]() r,
r,
即為d![]() r,即有
r,即有![]()
![]() .
.
可得![]() ,
,
e![]() .
.
另解:可得△PAQ為等邊三角形,
設OP=x,可得
設M為PQ的中點,可得PM=x,AM![]() x,
x,
tan∠MOA![]() ,
,
則e![]() .
.
故選:C.


科目:高中數學 來源: 題型:
【題目】如圖,五面體A﹣BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四邊形BCC1B1是矩形,二面角A﹣BC﹣C1為直二面角.
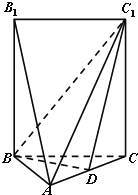
(1)D在AC上運動,當D在何處時,有AB1//平面BDC1,并且說明理由;
(2)當AB1//平面BDC1時,求二面角C﹣BC1﹣D余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為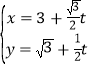 (
(![]() 為參數),點
為參數),點![]() 的極坐標為
的極坐標為![]() ,設直線
,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在底面是菱形的四棱錐![]() 中,
中,![]() ,點E在PD上,且
,點E在PD上,且![]() .
.

(1)證明:![]() 平面ABCD;
平面ABCD;
(2)求二面角![]() 的大小;
的大小;
(3)棱PC上是否存在一點F,使![]() 平面AEC?證明你的結論.
平面AEC?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,兩焦點與短軸的一個端點的連線構成的三角形面積為
,兩焦點與短軸的一個端點的連線構成的三角形面積為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設與圓O:![]() 相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com