Question

【題目】已知函數f（x）=ax2﹣2ax+b（a＞0）在區間[﹣1，4]上有最大值10和最小值1．設g（x）= ．
（1）求a、b的值；
（2）證明：函數g（x）在[ ，+∞）上是增函數；
（3）若不等式g（2x）﹣k2x≥0在x∈[﹣1，1]上有解，求實數k的取值范圍．

Answer 1

【答案】
（1）解：f（x）=a（x﹣1）2﹣a+b，（a＞0），

因為a＞0，故 ，解得

（2）證明：由已知可得g（x）=x+ ﹣2，設 ≤x1＜x2，

∵g（x1）﹣g（x2）=（x1﹣x2）（1﹣ ）=

∵ ≤x1＜x2，∴x1﹣x2＜0，2＜x1x2，即x1x2﹣2＞0．

∴g（x1）﹣g（x2）＜0，即g（x1）＜g（x2）．

所以函數g（x）在[ ，+∞）上是增函數

（3）解：g（2x）﹣k2x≥0可化為2x+ ﹣2≥k2x，

化為1+2 ﹣2 ≥k，

令t= ，則k≤2t2﹣2t+1，

因x∈[﹣1，1]，故t∈[ ，2]，

記h（t）=2t2﹣2t+1，因為t∈[ ，2]，故h（t）max=5，

所以k的取值范圍是（﹣∞，5]

【解析】（1）根據函數的對稱軸得到關于a的方程組，解出即可；（2）先求出g（x）的表達式，根據定義證明函數的單調性即可；（3）問題轉化為1+2 ﹣2 ≥k，令t= ，則k≤2t2﹣2t+1，構造新函數，結合函數的單調性從而求出k的范圍即可．
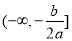【考點精析】解答此題的關鍵在于理解函數單調性的判斷方法的相關知識，掌握單調性的判定法：①設x1,x2是所研究區間內任兩個自變量，且x1＜x2；②判定f(x1)與f(x2)的大小；③作差比較或作商比較，以及對二次函數的性質的理解，了解當時，拋物線開口向上，函數在上遞減，在上遞增；當時，拋物線開口向下，函數在上遞增，在上遞減．