【題目】第31屆夏季奧林匹克運動會將于2016年8月5日—21日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據（單位：枚）.
（Ⅰ）根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖，并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度（不要求計算出具體數值，給出結論即可）；
（Ⅱ）甲、乙、丙三人競猜今年中國代表團和俄羅斯代表團中的哪一個獲得的金牌數多（假設兩國代表團獲得的金牌數不會相等），規定甲、乙、丙必須在兩個代表團中選一個，已知甲、乙猜中國代表團的概率都為
，丙猜中國代表團的概率為
，三人各自猜哪個代表團的結果互不影響.現讓甲、乙、丙各猜一次，設三人中猜中國代表團的人數為
，求
的分布列及數學期望
.
【答案】(Ⅰ)莖葉圖見解析，中國代表團獲得的金牌數的平均值高于俄羅斯代表團獲得的金牌數的平均值，俄羅斯代表團獲得的金牌數比較集中，中國代表團獲得的金牌數比較分散；(Ⅱ)分布列見解析，
.
【解析】
試題分析：(Ⅰ)觀察莖葉圖,運用平均數公式計算并比較即可；(Ⅱ)借助題設條件,運用求獨立事件和對立事件的公式分別求解即可.
試題解析:
（Ⅰ）兩國代表團獲得的金牌數的莖葉圖如下
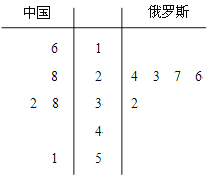
通過莖葉圖可以看出，中國代表團獲得的金牌數的平均值高于俄羅斯代表團獲得的金牌數的平均值；俄羅斯代表團獲得的金牌數比較集中，中國代表團獲得的金牌數比較分散。
（Ⅱ）解：
的可能取值為
，設事件
分別表示甲、乙、丙猜中國代表團，則
故的分布列為
小學生10分鐘口算測試100分系列答案科目：高中數學 來源： 題型：
【題目】某保險公司有一款保險產品的歷史收益率（收益率=利潤÷保費收入）的頻率分布直方圖如圖所示：
（Ⅰ）試估計平均收益率；
（Ⅱ）根據經驗，若每份保單的保費在20元的基礎上每增加
元，對應的銷量
（萬份）與
（元）有較強線性相關關系，從歷史銷售記錄中抽樣得到如下5組
與
的對應數據：
據此計算出的回歸方程為
.
（i）求參數
的估計值；
（ii）若把回歸方程
當作
與
的線性關系，用（Ⅰ）中求出的平均收益率估計此產品的收益率，每份保單的保費定為多少元時此產品可獲得最大收益，并求出該最大收益.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態度，選了某小區的100位居民調查結果統計如下:
（1）根據已有數據，把表格數據填寫完整；
（2）能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關？
（3）已知在被調查的年齡大于50歲的支持者中有5名女性，其中2位是女教師,現從這5名女性中隨機抽取3人，求至多有1位教師的概率.
附: 
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現階段全國多地空氣質量指數“爆表”.為探究車流量與
濃度是否相關，現對北方某中心城市的車流量最大的地區進行檢測，現采集到
月某天
個不同時段車流量與
濃度的數據，如下表：
車流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）根據上表中的數據，用最小二乘法求出
關于
的線性回歸方程；
（2）規定當
濃度平均值在
，空氣質量等級為優；當
濃度平均值在
，空氣質量等級為良；為使該城市空氣質量為優和良，利用該回歸方程，預測要將車流量控制在每小時多少萬輛內（結果以萬輛做單位，保留整數）.
附：回歸直線方程： 
，其中
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}中，a1＝
，前n項和Sn滿足Sn＋1－Sn＝(
)n＋1(n∈N*)．
(1)求數列{an}的通項公式an以及前n項和Sn；
(2)若S1，t(S1＋S2)，3(S2＋S3)成等差數列，求實數t的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}滿足a1=1，nan+1=（n+1）an+n（n+1），n∈N* ． （Ⅰ）證明：數列{ 
}是等差數列；
（Ⅱ）設bn=3n 
，求數列{bn}的前n項和Sn ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
