【題目】如圖，直三棱柱
中，
，
，
，
，點D，E分別為AB，
的中點．
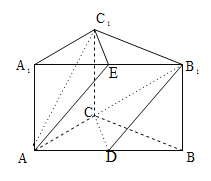
（1）求證：平面
平面
；
（2）求異面直線
與
所成角的余弦值．
【答案】（1）證明見解析；（2）
．
【解析】
（1）只要證出
，
，根據面面平行的判定定理，即可得到平面
平面
；
（2）根據中位線平移法，連接
交
于O，即可得到
即為異面直線
與所成的角或其補角，再根據題意解三角形即可求出．
（1）∵D、E分別為AB、
的中點，
∴
且
∴四邊形
為平行四邊形
∴，又
平面，
平面
∴
平面．
連接DE，
∵D、E分別為AB，的中點，∴
，且
又
且
，∴
，且
∴四邊形
為平行四邊形，
∴∵，
平面，
平面，
則有
平面．
又
，∴平面平面．
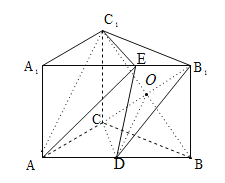
（2）連接交于O，易證
且
．
∴即為異面直線與所成的角或其補角．
在三角形ABC中，
，
，
，
則
為直角三角形，AB為斜邊，
即有
，
，
，
在三角形CDO中，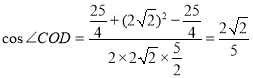
，
所以異面直線與所成角的余弦值．
七彩題卡口算應用一點通系列答案科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P-ABCD中，底面ABCD是邊長為3的菱形，∠ABC=60°．PA⊥面ABCD，且PA=3．F在棱PA上，且AF=1，E在棱PD上．
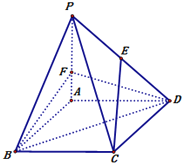
（Ⅰ）若CE∥面BDF，求PE：ED的值；
（Ⅱ）求二面角B-DF-A的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，幾何體AMDCNB是由兩個完全相同的四棱錐構成的幾何體，這兩個四棱錐的底面ABCD為正方形，
，平面
平面ABCD.
(1)證明:平面
平面MDC.
(2)若
，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某市高三數學復習備考情況，該市教研機構組織了一次檢測考試，并隨機抽取了部分高三理科學生數學成績繪制如圖所示的頻率分布直方圖.
（1）根據頻率分布直方圖，估計該市此次檢測理科數學的平均成績
；（精確到個位）
（2）研究發現，本次檢測的理科數學成績
近似服從正態分布
（
，
約為
），按以往的統計數據，理科數學成績能達到自主招生分數要求的同學約占
.
（ⅰ）估計本次檢測成績達到自主招生分數要求的理科數學成績大約是多少分？（精確到個位）
（ⅱ）從該市高三理科學生中隨機抽取
人，記理科數學成績能達到自主招生分數要求的人數為
，求的分布列及數學期望
．（說明：
表示
的概率.參考數據：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知傾斜角為
的直線
過點
和點
，在第一象限，
；
（1）求點的坐標；
（2）若直線與兩平行直線
，
相交于
兩點，且
，求實數
的值；
（3）對于平面上任一點
，當點
在線段
上運動時，稱
的最小值為與線段的距離，試求點
，
到線段的距離
關于
的函數關系式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四邊形ABCD是平行四邊形，點P是平面ABCD外一點，M是PC的中點，在DM上取一點G，過G和AP的平面交平面BDM于GH，H在BD上．
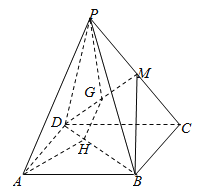
（1）求證
平面BDM．
（2）若G為DM中點，求證：
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
