【題目】已知函數
.
（1）當
時，求函數
的單調區間；
（2）當
時，若函數在
上的最小值為0，求
的值；
（3）當時，若函數在
上既有最大值又有最小值，且
恒成立，求實數
的取值范圍.
【答案】（1）單調遞減區間為
；（2）
或
；（3）
或
.
【解析】
（1）將
代入函數解析式，去掉絕對值符號，將函數寫出分段函數的形式，結合二次函數的單調性，寫出函數的單調遞減區間；
（2）將函數解析式化為分段函數的形式，對
的范圍進行討論，從而確定函數的最小值點，相互對照，求得結果；
（3）首先根據題意，判斷出函數在區間上存在最值的條件，利用恒成立，轉化得出對應的不等關系，進而求得其范圍.
（1）當時，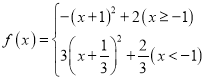
由二次函數單調性知
在
單調遞減，在
單調遞減，
∴的單調遞減區間為
（2）
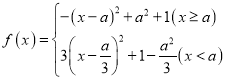
當
時，在
單調遞減，
單調遞增，
單調遞減，
（i）當
即
時，
∴
（舍去）
（ii）由
得
當
，即
時，
∴，符合題意.
（iii）當
，即
時，
∴，符合題意.
綜上所述，或.
（3）當時，由
，可知
由
可知
要使
恒成立
∵
又∵
∴
，∴
∴或.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】目前，某市出租車的計價標準是：路程2
以內（含2）按起步價8元收取，超過2后的路程按1.9元／km收取，但超過15后的路程需加收50%的返空費（即單價為
元／）．
（1）若
，將乘客搭乘-次出租車的費用
（單價：元）表示為行程
（單位：）的分段函數；
（2）某乘客行程為16，他準備先乘一輛出租車行駛8，然后再換乘另一輛出租車完成余下路程，請問：他這樣做是否比只乘一輛出租車完成全程更省錢？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
,
是兩條不同的直線, 
,
,
是三個不同的平面．有下列四個命題：
①若
，
，
，則
； ②若
，
，則
；
③ 若
，
，，則
；④ 若
，
，，則．
其中錯誤命題的序號是
A. ①③ B. ①④ C. ②③④ D. ②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學共有1000名學生參加了該地區高三第一次質量檢測的數學考試，數學成績如下表所示：
數學成績分組 | [0，30） | [30，60） | [60，90） | [90，120） | [120，150] |
人數 | 60 | 90 | 300 | x | 160 |
（Ⅰ）為了了解同學們前段復習的得失，以便制定下階段的復習計劃，學校將采用分層抽樣的方法抽取100名同學進行問卷調查，甲同學在本次測試中數學成績為95分，求他被抽中的概率；
（Ⅱ）作出頻率分布直方圖，并估計該學校本次考試的數學平均分．（同一組中的數據用該組區間的中點值作代表）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國家射擊隊的某隊員射擊一次，命中7~10環的概率如表所示：
命中環數 | 10環 | 9環 | 8環 | 7環 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該射擊隊員射擊一次 求:
（1）射中9環或10環的概率；
（2）至少命中8環的概率；（3）命中不足8環的概率。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
