
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,且橢圓
軸上,且橢圓![]() 的焦距為2.
的焦距為2.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,過
,過![]() 作
作![]() 軸且與橢圓
軸且與橢圓![]() 交于另一點
交于另一點![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,求證:三點
的右焦點,求證:三點![]() 在同一條直線上.
在同一條直線上.
 全能測控一本好卷系列答案
全能測控一本好卷系列答案 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:
【題目】設![]() 點為圓
點為圓![]() 上的動點,點
上的動點,點![]() 在
在![]() 軸上的投影為
軸上的投影為![]() ,動點
,動點![]() 滿足
滿足![]() ,動點
,動點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設![]() 的左頂點為
的左頂點為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,
,![]() (
(![]() ,
,![]() 不是左右頂點),且滿足
不是左右頂點),且滿足![]() ,求證:直線
,求證:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=2x和g(x)=2x的圖象如圖所示,設兩函數的圖象交于點A(x1,y1),B(x2,y2),且x1<x2.

(1)請指出圖中曲線C1,C2分別對應的函數;
(2)結合函數圖象,判斷![]() 與
與![]() ,f(2 019)與g(2 019)的大小.
,f(2 019)與g(2 019)的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市在節日期間進行有獎促銷,凡在該超市購物滿![]() 元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有
元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有![]() 只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵
只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵![]() 元;共兩只球都是綠色,則獎勵
元;共兩只球都是綠色,則獎勵![]() 元;若兩只球顏色不同,則不獎勵.
元;若兩只球顏色不同,則不獎勵.
(1)求一名顧客在一次摸獎活動中獲得![]() 元的概率;
元的概率;
(2)記![]() 為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量
為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位用2160萬元購得一塊空地,計劃在該空地上建造一棟至少10層,每層2000平方米的樓房.經測算,如果將樓房建為x(x≥10)層,則每平方米的平均建筑費用為560+48x(單位:元).
(1)寫出樓房平均綜合費用y關于建造層數x的函數關系式;
(2)該樓房應建造多少層時,可使樓房每平方米的平均綜合費用最少?最少值是多少?
(注:平均綜合費用=平均建筑費用+平均購地費用,平均購地費用=購地總費用/建筑總面積)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 既有一個極小值又有一個極大值,求
既有一個極小值又有一個極大值,求![]() 的取值范圍;
的取值范圍;
(3)若存在![]() ,使得當
,使得當![]() 時,
時, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據市場調查,某種商品一年內每件出廠價在6千元的基礎上,按月呈![]() 的模型波動(x為月份),已知3月份達到最高價8千元,7月份價格最低為4千元,該商品每件的售價為
的模型波動(x為月份),已知3月份達到最高價8千元,7月份價格最低為4千元,該商品每件的售價為![]() (x為月份),且滿足
(x為月份),且滿足![]() .
.
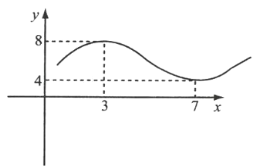
(1)分別寫出該商品每件的出廠價函數![]() 和售價函數
和售價函數![]() 的解析式;
的解析式;
(2)問幾月份的銷售盈利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com