
【題目】某名校從![]() 年到
年到![]() 年考入清華,北大的人數可以通過以下表格反映出來。(為了方便計算,將
年考入清華,北大的人數可以通過以下表格反映出來。(為了方便計算,將![]() 年編號為
年編號為![]() ,
,![]() 年編為
年編為![]() ,以此類推……)
,以此類推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人數 |
|
|
|
|
|
|
|
|
|
|
(1)將這![]() 年的數據分為人數不少于
年的數據分為人數不少于![]() 人和少于
人和少于![]() 人兩組,按分層抽樣抽取
人兩組,按分層抽樣抽取![]() 年,問考入清華、北大的人數不少于20的應抽多少年?在抽取的這
年,問考入清華、北大的人數不少于20的應抽多少年?在抽取的這![]() 年里,若隨機的抽取兩年恰有一年考入清華、北大的人數不少于
年里,若隨機的抽取兩年恰有一年考入清華、北大的人數不少于![]() 的概率是多少?;
的概率是多少?;
(2)根據最近![]() 年的數據,利用最小二乘法求出與之間的線性回歸方程,并用以預測
年的數據,利用最小二乘法求出與之間的線性回歸方程,并用以預測![]() 年該校考入清華、北大的人數。(結果要求四舍五入至個位)
年該校考入清華、北大的人數。(結果要求四舍五入至個位)
參考公式: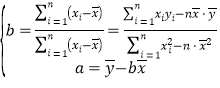
【答案】(1)![]() 年,
年,![]()
(2)![]() 與
與![]() 之間的線性回歸方程
之間的線性回歸方程![]() ,預測
,預測![]() 年該校考入清華,北大的人數為
年該校考入清華,北大的人數為![]() 人。
人。
【解析】
(1)先統計出人數少于20人有幾年,人數不少于20人的有幾年,這樣按分層抽樣抽取5年,這樣就可以求出考入清華、北大的人數不少于5的應抽多少年,然后求出隨機的抽取兩年恰有一年考入清華、北大的人數不少于![]() 的概率。
的概率。
(2)按照公式求出![]() ,最后求出
,最后求出![]() 與
與![]() 之間的線性回歸方程,當
之間的線性回歸方程,當![]() ,代入線性回歸方程中,就可預測
,代入線性回歸方程中,就可預測![]() 年該校考入清華、北大的人數。(格外要注意結果要求四舍五入至個位)
年該校考入清華、北大的人數。(格外要注意結果要求四舍五入至個位)
(1)在這10年里,人數不少于![]() 人有4年,少于20人的有6年,分層抽樣抽取5年,所以抽取人數不少于
人有4年,少于20人的有6年,分層抽樣抽取5年,所以抽取人數不少于![]() 人有2年,少于20人的有3年;隨機的抽取兩年恰有一年考入清華、北大的人數不少于
人有2年,少于20人的有3年;隨機的抽取兩年恰有一年考入清華、北大的人數不少于![]() 為事件
為事件![]() ,則
,則![]() 。
。
(2)計算出![]() ,代入所給的公式中,
,代入所給的公式中,
得![]() ,
,![]() 與
與![]() 之間的線性回歸方程
之間的線性回歸方程![]() ,當
,當![]() 時,
時,![]() ,
,
所以![]() 與
與![]() 之間的線性回歸方程
之間的線性回歸方程![]() ,預測
,預測![]() 年該校考入清華,北大的人數為
年該校考入清華,北大的人數為![]() 人。
人。


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】判斷下列命題的真假:
(1)![]() 是有理數;(2)
是有理數;(2)![]() ;
;
(3)奇數的平方仍是奇數;(4)兩個集合的交集還是一個集合;
(5)每一個素數都是奇數;(6)方程![]() 有實數根;
有實數根;
(7)![]() ;(8)如果
;(8)如果![]() ,那么
,那么![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班共有學生45人,其中女生18人,現用分層抽樣的方法,從男、女學生中各抽取若干學生進行演講比賽,有關數據見下表(單位:人)
性別 | 學生人數 | 抽取人數 |
女生 | 18 |
|
男生 |
| 3 |
(1)求![]() 和
和![]() ;
;
(2)若從抽取的學生中再選2人做專題演講,求這2人都是男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩家銷售公司擬各招聘一名產品推銷員,日工資方案如下: 甲公司規定底薪80元,每銷售一件產品提成1元; 乙公司規定底薪120元,日銷售量不超過45件沒有提成,超過45件的部分每件提成8元.
(I)請將兩家公司各一名推銷員的日工資![]() (單位: 元) 分別表示為日銷售件數
(單位: 元) 分別表示為日銷售件數![]() 的函數關系式;
的函數關系式;
(II)從兩家公司各隨機選取一名推銷員,對他們過去100天的銷售情況進行統計,得到如下條形圖。若記甲公司該推銷員的日工資為![]() ,乙公司該推銷員的日工資為
,乙公司該推銷員的日工資為![]() (單位: 元),將該頻率視為概率,請回答下面問題:
(單位: 元),將該頻率視為概率,請回答下面問題:
某大學畢業生擬到兩家公司中的一家應聘推銷員工作,如果僅從日均收入的角度考慮,請你利用所學的統計學知識為他作出選擇,并說明理由.
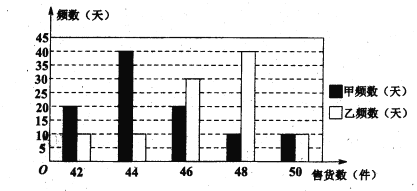
【答案】(I)見解析; (Ⅱ)見解析.
【解析】分析:(I)依題意可得甲公司一名推銷員的工資與銷售件數的關系是一次函數的關系式,而乙公司是分段函數的關系式,由此解得;(Ⅱ)分別根據條形圖求得甲、乙公司一名推銷員的日工資的分布列,從而可分別求得數學期望,進而可得結論.
詳解:(I)由題意得,甲公司一名推銷員的日工資![]() (單位:元) 與銷售件數
(單位:元) 與銷售件數![]() 的關系式為:
的關系式為: ![]() .
.
乙公司一名推銷員的日工資![]() (單位: 元) 與銷售件數
(單位: 元) 與銷售件數![]() 的關系式為:
的關系式為: 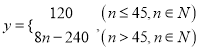
(Ⅱ)記甲公司一名推銷員的日工資為![]() (單位: 元),由條形圖可得
(單位: 元),由條形圖可得![]() 的分布列為
的分布列為
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
記乙公司一名推銷員的日工資為![]() (單位: 元),由條形圖可得
(單位: 元),由條形圖可得![]() 的分布列為
的分布列為
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴僅從日均收入的角度考慮,我會選擇去乙公司.
點睛:求解離散型隨機變量的數學期望的一般步驟為:
第一步是“判斷取值”,即判斷隨機變量的所有可能取值,以及取每個值所表示的意義;
第二步是“探求概率”,即利用排列組合,枚舉法,概率公式,求出隨機變量取每個值時的概率;
第三步是“寫分布列”,即按規范形式寫出分布列,并注意用分布列的性質檢驗所求的分布列或某事件的概率是否正確;
第四步是“求期望值”,一般利用離散型隨機變量的數學期望的定義求期望的值
【題型】解答題
【結束】
19
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.
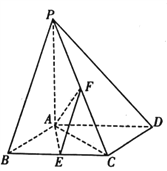
(1)證明: ![]() ;
;
(2)設![]() 為線段
為線段![]() 上的動點,若線段
上的動點,若線段![]() 長的最小值為
長的最小值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() , (
, (![]() 為參數,
為參數, ![]() 為傾斜角).以坐標原點為極點,
為傾斜角).以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
(Ⅰ)將曲線![]() 的直角坐標方程化為極坐標方程;
的直角坐標方程化為極坐標方程;
(Ⅱ)設點![]() 的直角坐標為
的直角坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】試題分析:(Ⅰ)將由![]() 代入
代入![]() ,化簡即可得到曲線
,化簡即可得到曲線![]() 的極坐標方程;(Ⅱ)將
的極坐標方程;(Ⅱ)將![]() 的參數方程
的參數方程![]() 代入
代入![]() ,得
,得![]() ,根據直線參數方程的幾何意義,利用韋達定理結合輔助角公式,由三角函數的有界性可得結果.
,根據直線參數方程的幾何意義,利用韋達定理結合輔助角公式,由三角函數的有界性可得結果.
試題解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲線![]() 的極坐標方程為
的極坐標方程為![]()
(II)將![]() 的參數方程
的參數方程![]() 代入
代入![]() ,得
,得![]()
∴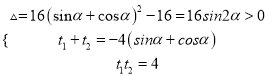 , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范圍是
的取值范圍是![]() .
.
【題型】解答題
【結束】
23
【題目】已知![]() 、
、![]() 、
、![]() 均為正實數.
均為正實數.
(Ⅰ)若![]() ,求證:
,求證: ![]()
(Ⅱ)若![]() ,求證:
,求證: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年電子商務蓬勃發展, ![]() 年某網購平臺“雙
年某網購平臺“雙![]() ”一天的銷售業績高達
”一天的銷售業績高達![]() 億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出
億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出![]() 次成功交易,并對其評價進行統計,網購者對商品的滿意率為
次成功交易,并對其評價進行統計,網購者對商品的滿意率為![]() ,對快遞的滿意率為
,對快遞的滿意率為![]() ,其中對商品和快遞都滿意的交易為
,其中對商品和快遞都滿意的交易為![]() 次.
次.
(1)根據已知條件完成下面的![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
對快遞滿意 | 對快遞不滿意 | 合計 | |
對商品滿意 |
| ||
對商品不滿意 | |||
合計 |
|
(2)為進一步提高購物者的滿意度,平臺按分層抽樣方法從中抽取![]() 次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這
次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這![]() 次交易中再隨機抽取
次交易中再隨機抽取![]() 次進行電話回訪,聽取購物者意見.求電話回訪的
次進行電話回訪,聽取購物者意見.求電話回訪的![]() 次交易至少有一次對商品和快遞都滿意的概率.
次交易至少有一次對商品和快遞都滿意的概率.
附: 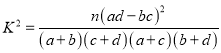 (其中
(其中![]() 為樣本容量)
為樣本容量)
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
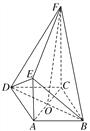
【題目】已知三棱錐![]() (如圖1)的平面展開圖(如圖2)中,四邊形
(如圖1)的平面展開圖(如圖2)中,四邊形![]() 為邊長為
為邊長為![]() 的正方形,△ABE和△BCF均為正三角形,在三棱錐
的正方形,△ABE和△BCF均為正三角形,在三棱錐![]() 中:
中:
(I)證明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若點![]() 在棱
在棱![]() 上,滿足
上,滿足![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函數f(x)的圖象在x=1處的切線與x軸平行,求f(x)的單調區間;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范圍.
,+∞)上恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,菱形ABCD中,∠ABC=60°,AC與BD相交于點O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
(1)求證:BD⊥平面ACFE;
(2)當直線FO與平面BED所成的角為45°時,求異面直線OF與BE所成的角的余弦值大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com