
【題目】在三棱柱![]() 中,側面
中,側面![]() 為矩形,
為矩形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,
的中點, ![]() 與
與![]() 交于點
交于點![]() ,且
,且![]() 平面
平面![]() .
.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 的重心為
的重心為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)通過證明![]() ,
, ![]() ,推出
,推出![]() 平面
平面![]() ,然后證明平面
,然后證明平面![]() 平面
平面![]() .(2)以
.(2)以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() ,
, ![]() ,
, ![]() 軸建立如圖所示的空間直角坐標系
軸建立如圖所示的空間直角坐標系![]() .求出平面
.求出平面![]() 的法向量,設直線
的法向量,設直線![]() 與平面
與平面![]() 所成角
所成角![]() ,利用空間向量的數量積求解直線
,利用空間向量的數量積求解直線![]() 與平面
與平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
試題解析:(1)∵![]() 為矩形,
為矩形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,
的中點,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
從而![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,從而
,從而![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
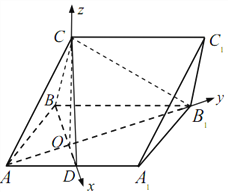
(2)如圖,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() ,
, ![]() ,
, ![]() 軸建立如圖所示的空間直角坐標系
軸建立如圖所示的空間直角坐標系![]() .
.
在矩形![]() 中,由于
中,由于![]() ,所以
,所以![]() 和
和![]() 相似,
相似,
從而![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴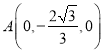 ,
, 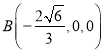 ,
, 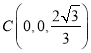 ,
,  ,
,  ,
,
∵![]() 為
為![]() 的重心,∴
的重心,∴ ,
, 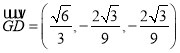 ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
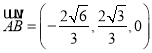 ,
, 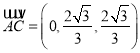 ,
,
由![]() 可得
可得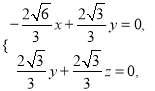 整理得
整理得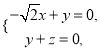
令![]() ,則
,則![]() ,
, ![]() ,∴
,∴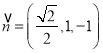 ,
,
設直線![]() 與平面
與平面![]() 所成角
所成角![]() ,則
,則
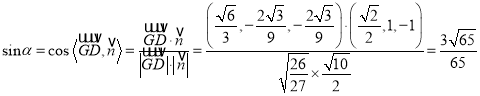 ,
,
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知D,E,F分別為△ABC的邊BC,CA,AB的中點,記 ![]() =a ,
=a , ![]() =b.則下列命題中正確的個數是( )
=b.則下列命題中正確的個數是( )
① ![]() =
= ![]() a-b;②
a-b;② ![]() =a+
=a+ ![]() b;③
b;③ ![]() =
= ![]() a+
a+ ![]() b;④
b;④ ![]() 0.
0.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+3x+a
(1)當a=﹣2時,求不等式f(x)>2的解集
(2)若對任意的x∈[1,+∞),f(x)>0恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga ![]() (a>0,a≠1,m≠﹣1),是定義在(﹣1,1)上的奇函數.
(a>0,a≠1,m≠﹣1),是定義在(﹣1,1)上的奇函數.
(1)求f(0)的值和實數m的值;
(2)當m=1時,判斷函數f(x)在(﹣1,1)上的單調性,并給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ax2+2(a﹣3)x+1在區間[﹣2,+∞)上遞減,則實數a的取值范圍是( )
A.(﹣∞,﹣3]
B.[﹣3,0]
C.[﹣3,0)
D.[﹣2,0]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,點D是AB的中點. 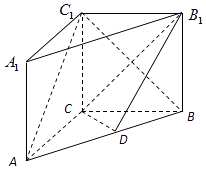
(1)求證:AC⊥BC1;
(2)求證:AC1∥平面CDB1;
(3)求二面角B﹣DC﹣B1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒中有6只燈泡,其中有2只是次品,4只是正品.從中任取2只,試求下列事件的概率.
(Ⅰ)取到的2只都是次品;
(Ⅱ)取到的2只中恰有一只次品.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,2,在Rt△ABC中,AB=BC=4,點E在線段AB上,過點E作交AC于點F,將△AEF沿EF折起到△PEF的位置(點A與P重合),使得∠PEB=60°. 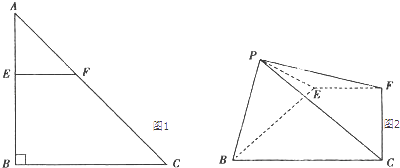
(1)求證:EF⊥PB;
(2)試問:當點E在何處時,四棱錐P﹣EFCB的側面的面積最大?并求此時四棱錐P﹣EFCB的體積及直線PC與平面EFCB所成角的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com