【題目】某超市周年慶典，設置了一項互動游戲如圖，一個圓形游戲轉(zhuǎn)盤被分成6個均勻的扇形區(qū)域.用力旋轉(zhuǎn)轉(zhuǎn)盤，轉(zhuǎn)盤停止轉(zhuǎn)動時，箭頭
所指區(qū)域的數(shù)字就是每次游戲所得的分數(shù)（箭頭指向兩個區(qū)域的邊界時重新轉(zhuǎn)動），且箭頭指向每個區(qū)域的可能性都是相等的.要求每個家庭派一名兒童和一位成人先后各轉(zhuǎn)動一次游戲轉(zhuǎn)盤，記為
，若一個家庭總得分
,假設兒童和成人的得分互不影響，且每個家庭只能參加一次活動，游戲規(guī)定：
①若
，則該家庭可以獲得一等獎一份；
②若
，則該家庭可以獲得二等獎一份；
若
，則該家庭可以獲得紀念獎一份.
(1)求一個家庭獲得紀念獎的概率；
(2)試比較同一個家庭獲得一等獎和二等獎概率的大小.
【答案】（1）一個家庭獲得紀念獎的概率為
；（2）見解析.
【解析】試題分析：（1）利用枚舉法確定獲得紀念獎的情況，再根據(jù)古典概型概率公式求概率，（2）利用枚舉法確定獲得一等獎和二等獎的情況，再根據(jù)古典概型概率公式求概率，最后比較大小.
試題解析：(1)由題意可知，一個家庭的得分情況共有 36 種，獲得紀念獎的情況為
.共有19種.
記事件
“一個家庭獲得紀念獎”，則
.
故一個家庭獲得紀念獎的概率為.
(2)記事件
“一個家庭獲得一等獎”,則符合獲得一等獎條件的得分情況包括：
共3種，則
.
記事件
“一個家庭獲得二等獎”,則符合獲得二等獎條件的得分情況包括：
共3種，所以
.
所以同一個家庭獲得一等獎和二等獎的概率相等．
科目：高中數(shù)學 來源： 題型：
【題目】已知集合A＝{x|x2－2x－3≤0}，B＝{x|x2－2mx＋m2－4≤0，x∈R，m∈R}．
(1)若A∩B＝[0,3]，求實數(shù)m的值；
(2)若ARB，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在一次詩詞知識競賽調(diào)查中，發(fā)現(xiàn)參賽選手分為兩個年齡（單位:歲）段：
，
，其中答對詩詞名句與否的人數(shù)如圖所示.
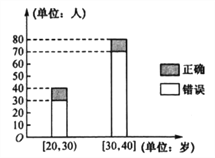
（1）完成下面2×2列聯(lián)表；
年齡段 | 正確 | 錯誤 | 合計 |
| |||
| |||
合計 |
（2）是否有90%的把握認為答對詩詞名句與年齡有關，請說明你的理由；
（3）現(xiàn)按年齡段分層抽樣選取6名選手，若從這6名選手中選取3名選手，求3名選手中年齡在歲范圍人數(shù)的分布列和數(shù)學期望.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某省的一個氣象站觀測點在連續(xù)4天里記錄的AQI指數(shù)M與當天的空氣水平可見度
（單位：cm）的情況如表1：
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
該省某市2017年11月份AQI指數(shù)頻數(shù)分布如表2：
|
|
|
|
|
|
頻數(shù)（天） | 3 | 6 | 12 | 6 | 3 |
<>（1）設
，若
與之間是線性關系，試根據(jù)表1的數(shù)據(jù)求出關于的線性回歸方程；（2）小李在該市開了一家洗車店，洗車店每天的平均收入與AQI指數(shù)存在相關關系如表3：
|
|
|
|
|
|
日均收入（元） | -2000 | -1000 | 2000 | 6000 | 8000 |
根據(jù)表3估計小李的洗車店2017年11月份每天的平均收入.
附參考公式：
，其中
，
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的離心率為
，點
在橢圓
上.
(1)求橢圓的方程；
(2)若不過原點
的直線
與橢圓相交于
兩點，與直線
相交于點
，且是線段
的中點，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)f（x）=（1-x2）ex．
（1）討論f（x）的單調(diào)性；
（2）當x≥0時，f（x）≤ax+1，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】對于集合
和常數(shù)
，定義：
為集合
相對的“余弦方差”.
（1）若集合
，
，求集合相對的“余弦方差”；
（2）求證：集合
相對任何常數(shù)的“余弦方差”是一個與無關的定值，并求此定值；
（3）若集合
，
，
，相對任何常數(shù)的“余弦方差”是一個與無關的定值，求出
、
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
