
【題目】某中學對男女學生是否喜愛古典音樂進行了一個調查,調查者對學校高三年級隨機抽取了100名學生,調查結果如表:
喜愛 | 不喜愛 | 總計 | |
男學生 | 60 | 80 | |
女學生 | |||
總計 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根據表中數據,判斷是否有95%的把握認為“男學生和女學生喜歡古典音樂的程度有差異”;
(2)從以上被調查的學生中以性別為依據采用分層抽樣的方式抽取10名學生,再從這10名學生中隨機抽取5名學生去某古典音樂會的現場觀看演出,求正好有X個男生去觀看演出的分布列及期望.
【答案】
(1)解:2×2列聯表
喜愛 | 不喜愛 | 總計 | |
男學生 | 60 | 20 | 80 |
女學生 | 10 | 10 | 20 |
總計 | 70 | 30 | 100 |
∴K2= ![]() =
= ![]() ≈4.762>3.841,
≈4.762>3.841,
∴有95%的把握認為“男學生和女學生喜歡古典音樂的程度有差異”
(2)解:由題意,10名學生中有8名男生和2名女生,故X的取值為3,4,5.
P(X=3)= ![]() =
= ![]() ,P(X=4)=
,P(X=4)= ![]() =
= ![]() ,P(X=5)=
,P(X=5)= ![]() =
= ![]() ,
,
X的分布列
X | 3 | 4 | 5 |
P |
|
|
|
期望EX=3× ![]() +4×
+4× ![]() +5×
+5× ![]() =4
=4
【解析】(1)列出2×2列聯表,求出K2的值,判斷有95%的把握認為“男學生和女學生喜歡古典音樂的程度有差異”;(2)先確定X的取值,分別求其概率,求出分布列和數學期望.
【考點精析】根據題目的已知條件,利用分層抽樣的相關知識可以得到問題的答案,需要掌握先將總體中的所有單位按照某種特征或標志(性別、年齡等)劃分成若干類型或層次,然后再在各個類型或層次中采用簡單隨機抽樣或系用抽樣的辦法抽取一個子樣本,最后,將這些子樣本合起來構成總體的樣本.


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,所得圖象對應的函數
個單位長度,所得圖象對應的函數
A. 在區間![]() 上單調遞增 B. 在區間
上單調遞增 B. 在區間![]() 上單調遞減
上單調遞減
C. 在區間![]() 上單調遞增 D. 在區間
上單調遞增 D. 在區間![]() 上單調遞減
上單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 。
。
Ⅰ.求函數![]() 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
Ⅱ.當![]() 時,方程
時,方程![]() 恰有兩個不同的實數根,求實數
恰有兩個不同的實數根,求實數![]() 的取值范圍;
的取值范圍;
Ⅲ.將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后所得函數
個單位后所得函數![]() 的圖象關于原點中心對稱,求
的圖象關于原點中心對稱,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中, ![]() 為正三角形,平面
為正三角形,平面![]() 底面
底面![]() ,底面
,底面![]() 為梯形,
為梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() .
.
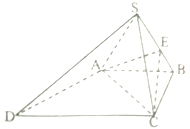
求證:(1)平面![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域為R,并且圖象關于y軸對稱,當x≤-1時,y=f(x)的圖象是經過點(-2,0)與(-1,1)的射線,又在y=f(x)的圖象中有一部分是頂點在(0,2),且經過點(1,1)的一段拋物線.
(1)試求出函數f(x)的表達式,作出其圖象;
(2)根據圖象說出函數的單調區間,以及在每一個單調區間上函數是增函數還是減函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x+1)e2x , g(x)=aln(x+1)+ ![]() x2+(3﹣a)x+a(a∈R).
x2+(3﹣a)x+a(a∈R).
(1)當a=9,求函數y=g(x)的單調區間;
(2)若f(x)≥g(x)恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一塊地皮![]() ,其中
,其中![]() ,
, ![]() 是直線段,曲線段
是直線段,曲線段![]() 是拋物線的一部分,且點
是拋物線的一部分,且點![]() 是該拋物線的頂點,
是該拋物線的頂點, ![]() 所在的直線是該拋物線的對稱軸.經測量,
所在的直線是該拋物線的對稱軸.經測量, ![]() km,
km, ![]() km,
km, ![]() .現要從這塊地皮中劃一個矩形
.現要從這塊地皮中劃一個矩形![]() 來建造草坪,其中點
來建造草坪,其中點![]() 在曲線段
在曲線段![]() 上,點
上,點![]() ,
, ![]() 在直線段
在直線段![]() 上,點
上,點![]() 在直線段
在直線段![]() 上,設
上,設![]() km,矩形草坪
km,矩形草坪![]() 的面積為
的面積為![]() km2.
km2.
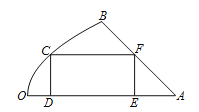
(1)求![]() ,并寫出定義域;
,并寫出定義域;
(2)當![]() 為多少時,矩形草坪
為多少時,矩形草坪![]() 的面積最大?
的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于某產品的明星代言費x(百萬元)和其銷售額y(百萬元),有如表的統計表格:
i | 1 | 2 | 3 | 4 | 5 | 合計 |
xi(百萬元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
wi(百萬元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
yi(百萬元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| ||||||
其中 ![]() .
.
(1)在坐標系中,作出銷售額y關于廣告費x的回歸方程的散點圖,根據散點圖指出:y=a+blnx,y=c+dx3哪一個適合作銷售額y關于明星代言費x的回歸類方程(不需要說明理由); 
(2)已知這種產品的純收益z(百萬元)與x,y有如下關系:x=0.2y﹣0.726x(x∈[1.00,2.00]),試寫出z=f(x)的函數關系式,試估計當x取何值時,純收益z取最大值?(以上計算過程中的數據統一保留到小數點第2位)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com