【題目】已知函數f（x）=x3+ax2+bx圖象與直線x﹣y﹣4=0相切于（1，f（1））
（1）求實數a，b的值；
（2）若方程f（x）=m﹣7x有三個解，求實數m的取值范圍．
【答案】
（1）解： x=1代入直線方程可得f（1）=﹣3，
函數f（x）=x3+ax2+bx，求導可得f′（x）=3x2+2ax+b，
根據題意可得 
，
解得 
；
（2）解：由（1）可得f（x）=x3+2x2﹣6x，所以方程等價于x3+2x2﹣6x=m﹣7x，即x3+2x2+x=m，
令h（x）=x3+2x2+x，
∴h′（x）=3x2+4x+1=（3x+1）（x+1），
令h′（x）=0，解得x=﹣ 
或x=﹣1．當x變化時，h′（x），h（x）的變化情況如下表：
x | （﹣∞，﹣1） | ﹣1 |
|
|
|
h′（x） | + | 0 | ﹣ | 0 | + |
h（x） | 單調遞增 | 0 | 單調遞減 |
| 單調遞增 |
要使x3+2x2+x=m有三個解，需要 
，
所以m的取值范圍是
【解析】（1）求出切點坐標，利用導數與函數值，即可得到結果．（2）求出函數的導數，通過導數為0，得到函數的單調性，通過函數的極值點，推出不等式組，得到結果．
【考點精析】通過靈活運用利用導數研究函數的單調性，掌握一般的,函數的單調性與其導數的正負有如下關系： 在某個區間
內，(1)如果
，那么函數
在這個區間單調遞增；(2)如果
，那么函數
在這個區間單調遞減即可以解答此題．
教材全解字詞句篇系列答案科目：高中數學 來源： 題型：
【題目】三棱錐P﹣ABC，底面ABC為邊長為2 
的正三角形，平面PBC⊥平面ABC，PB=PC=2，D為AP上一點，AD=2DP，O為底面三角形中心．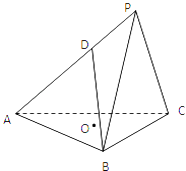 
（1）求證DO∥面PBC；
（2）求證：BD⊥AC；
（3）設M為PC中點，求平面MBD和平面BDO所成銳二面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點F1 ， F2分別是雙曲線 
的左、右焦點，過F1且垂直于x軸的直線與雙曲線交于A，B兩點，若△ABF2是銳角三角形，則該雙曲線離心率的取值范圍是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】全集U={﹣1，0，1，2，3，4，5，6 }，A={3，4，5 }，B={1，3，6 }，那么集合{ 2，﹣1，0}是（ ）
A.
B.
C.UA∩UB
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學在利用“五點法”作函數f（x）=Asin（ωx+）+t（其中A＞0， 
）的圖象時，列出了如表格中的部分數據．
x |
|
|
|
|
|
ωx+ | 0 | | π | | 2π |
f（x） | 2 | 6 | 2 | ﹣2 | 2 |
（1）請將表格補充完整，并寫出f（x）的解析式．
（2）若 
，求f（x）的最大值與最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數y=f（x）是R上的偶函數，且當x≤0時，f（x）=log 
（1﹣x）+x．
（1）求f（1）的值；
（2）求函數y=f（x）的表達式，并直接寫出其單調區間（不需要證明）；
（3）若f（lga）+2＜0，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a、b、c分別是△ABC的三個內角A、B、C的對邊．
（1）若△ABC面積S△ABC= 
，c=2，A=60°，求a、b的值；
（2）若a=ccosB，且b=csinA，試判斷△ABC的形狀．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
