Question

【題目】已知各項均為正數的兩個數列和{}滿足：an＋1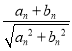＝，n∈N*.

(1)設bn＋1＝1＋，n∈N*，求證：數列是等差數列；

(2)設bn＋1＝·，n∈N*，且是等比數列，求a1和b1的值.

Answer 1

【答案】（1）見解析；（2）a1＝b1＝.

【解析】試題分析：（1）由an＋1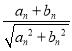＝，等式右邊分子分母同時除以，再將bn＋1＝1＋帶入可得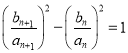，從而得證；

（2）由不等式性質有： 進而得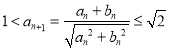，設等比數列{an}的公比為q，由反證法可得q＝1，故an＝a1(n∈N*)，所以1＜a1≤，從而得{bn}是公比為的等比數列,亦可由反證法得a1＝.

試題解析：

(1)證明　由題設知an＋1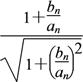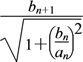＝＝＝，所以＝，

從而－＝1(n∈N*)，

所以數列是以1為公差的等差數列.

(2)解　因為an＞0，bn＞0，

所以≤a＋b＜(an＋bn)2，

從而1＜an＋1＝≤.(*)

設等比數列{an}的公比為q，由an＞0知q＞0.下證q＝1.

若q＞1，則a1＝＜a2≤，故當n＞logq時，an＋1＝a1qn＞，與(*)矛盾；

若0＜q＜1，則a1＝＞a2＞1，故當n＞logq時，an＋1＝a1qn＜1，與(*)矛盾.

綜上，q＝1，故an＝a1(n∈N*)，

所以1＜a1≤.

又bn＋1＝·＝·bn(n∈N*)，所以{bn}是公比為的等比數列.

若a1≠，則＞1，于是b1＜b2＜b3.

又由a1＝得bn＝ (n∈N*)，所以b1，b2，b3中至少有兩項相同，矛盾，

所以a1＝，從而bn＝＝.

所以a1＝b1＝.