【題目】如圖，
是正方形，點
在以
為直徑的半圓弧上（不與
，
重合），
為線段的中點，現(xiàn)將正方形沿折起，使得平面
平面
.
（1）證明：
平面
.
（2）若
，當三棱錐
的體積最大時，求到平面
的距離.
科目：高中數(shù)學 來源： 題型：
【題目】某地環(huán)保部門跟蹤調(diào)查一種有害昆蟲的數(shù)量．根據(jù)調(diào)查數(shù)據(jù)，該昆蟲的數(shù)量
（萬只）與時間
（年）（其中
）的關(guān)系為
．為有效控制有害昆蟲數(shù)量、保護生態(tài)環(huán)境，環(huán)保部門通過實時監(jiān)控比值
（其中
為常數(shù)，且
）來進行生態(tài)環(huán)境分析．
（1）當
時，求比值
取最小值時
的值；
（2）經(jīng)過調(diào)查，環(huán)保部門發(fā)現(xiàn)：當比值
不超過
時不需要進行環(huán)境防護．為確保恰好3年不需要進行保護，求實數(shù)
的取值范圍．（
為自然對數(shù)的底， 
）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】電子芯片是“中國智造”的靈魂，是所有整機設(shè)備的“心臟”.某國產(chǎn)電子芯片公司，通過大數(shù)據(jù)分析，得到如下規(guī)律：生產(chǎn)一種高端芯片x（
）萬片，其總成本為
，其中固定成本為800萬元，并且每生產(chǎn)1萬片的生產(chǎn)成本為200萬元（總成本=固定成本+生產(chǎn)成本），銷售收入
（單位：萬元）滿足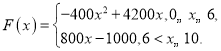
假定生產(chǎn)的芯片都能賣掉.
（1）將利潤
（單位：萬元）表示為產(chǎn)量x（單位：萬片）的函數(shù)；
（2）當產(chǎn)量x（單位：萬片）為何值時，公司所獲利潤最大？最大利潤為多少萬元？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）當
時，求
的單調(diào)區(qū)間.
（2）試問：是否存在實數(shù)
，使得
對
恒成立？若存在，求的取值范圍；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】一汽車廠生產(chǎn)
，
，
三類轎車，每類轎車均有舒適型和標準型兩種型號，某月的產(chǎn)量如下表(單位：輛)：按類用分層抽樣的方法在這個月生產(chǎn)的轎車中抽取50輛，其中有類轎車10輛．
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
（1）求
的值；
（2）用分層抽樣的方法在類轎車中抽取一個容量為5的樣本．將該樣本看成一個總體，從中任取2輛，求至少有1輛舒適型轎車的概率；
（3）用隨機抽樣的方法從類舒適型轎車中抽取8輛，經(jīng)檢測它們的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2 把這8輛轎車的得分看作一個總體，從中任取一個得分數(shù)
，記這8輛轎車的得分的平均數(shù)為
，定義事件
，且函數(shù)
沒有零點
，求事件
發(fā)生的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】沙漏是我國古代的一種計時工具，是用兩個完全相同的圓錐頂對頂疊放在一起組成的（如圖）.在一個圓錐中裝滿沙子，放在上方，沙子就從頂點處漏到另一個圓錐中，假定沙子漏下來的速度是恒定的.已知一個沙漏中沙子全部從一個圓錐中漏到另一個圓錐中需用時10分鐘.那么經(jīng)過5分鐘后，沙漏上方圓錐中的沙子的高度與下方圓錐中的沙子的高度之比是（假定沙堆的底面是水平的）（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的焦點為
，點
在拋物線
上，
為坐標原點，
，且
.
（1）求拋物線的方程；
（2）圓
與拋物線順次交于
四點，
所在的直線
過焦點，線段
是圓的直徑，
，求直線的方程..
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某品牌手機廠商推出新款的旗艦機型，并在某地區(qū)跟蹤調(diào)查得到這款手機上市時間（第
周）和市場占有率（
）的幾組相關(guān)數(shù)據(jù)如下表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）根據(jù)表中的數(shù)據(jù)，用最小二乘法求出
關(guān)于的線性回歸方程
；
（2）根據(jù)上述線性回歸方程，預(yù)測在第幾周，該款旗艦機型市場占有率將首次超過
（最后結(jié)果精確到整數(shù)）．
參考公式：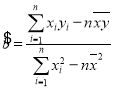
，
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知公差不等于
的正項等差數(shù)列
的前
項和為
，遞增等比數(shù)列
的前項和為
，
，
，
，
.
（1）求滿足
，
的
的最小值；
（2）求數(shù)列
的前項和
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
