【題目】設
.
（1）求
的單調區(qū)間；
（2）已知
，若對所有
，都有
成立，求實數(shù)
的取值范圍.
【答案】(I) 
上是增函數(shù).(II) 
【解析】試題分析：（1）對函數(shù)求導，后利用均值不等式易判斷導數(shù)值恒大于
，可得函數(shù)在定義域上單調遞增；（2）由已知整理可得
，可將原命題轉化為
成立，構造函數(shù)
，利用導數(shù)與函數(shù)單調性的關系，對
進行分討論后可得
的取值范圍．試題解析：
(I) 
，
∴在
上是增函數(shù).
(II) 
顯然
，故若使
，只需
即可.
令
，則
(i)當
即
時， 
恒成立，
∴
在
內(nèi)為增函數(shù)
∴
，即
在
上恒成立.
(ii)當
時，則令
，即
，可化為
，
解得
，
∴兩根
（舍），
從而
.
當
時，則
，
∴
，∴
在
為減函數(shù).
又
，∴
∴當
時， 
不恒成立，即
不恒成立.
綜上所述，a的取值范圍為
全能測控期末小狀元系列答案科目：高中數(shù)學 來源： 題型：
【題目】設全集U=R，集合A={x|﹣1≤x＜3}，B={x|2x﹣4≥x﹣2}．
（1）求U（A∩B）；
（2）若集合C={x|2x+a＞0}，滿足B∪C=C，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（Ⅰ）設不等式
對滿足
的一切實數(shù)
的取值都成立，求
的取值范圍；
（Ⅱ）是否存在實數(shù)
,使得不等式
對滿足
的一切實數(shù)
的取值都成立．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為加快新能源汽車產(chǎn)業(yè)發(fā)展，推進節(jié)能減排，國家對消費者購買新能源汽車給予補貼，其中對純電動乘車補貼標準如下表：
某校研究性學習小組，從汽車市場上隨機選取了
輛純電動乘用車，根據(jù)其續(xù)駛里程
（單次充電后能行駛的最大里程）作出了頻率與頻數(shù)的統(tǒng)計表：
（1）求
的值；
（2）若從這
輛純電動乘用車中任選3輛，求選到的3輛車續(xù)駛里程都不低于180公里的概率；
（3）如果以頻率作為概率，若某家庭在某汽車銷售公司購買了2輛純電動乘用車，設該家庭獲得的補貼為
（單位：萬元），求
的分布列和數(shù)學期望
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】長方體ABCD﹣A1B1C1D1中，AB=2，AA1=AD=4，點E為AB中點．
（1）求證：BD1∥平面A1DE；
（2）求證：A1D⊥平面ABD1 ．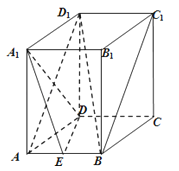 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
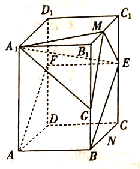
【題目】如圖，四邊形
是正四棱柱
的一個截面，此截面與棱
交于點
， 
,其中
分別為棱
上一點.
（1）證明：平面
平面
；
（2）
為線段
上一點，若四面體
與四棱錐
的體積相等，求
的長.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知以點C（t，
） （t∈R，t≠0）為圓心的圓與x軸交于點O、A，與y軸交于點O、B，其中O為原點．
（1）求證：△AOB的面積為定值；
（2）設直線2x+y﹣4=0與圓C交于點M、N，若OM=ON，求圓C的方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）若
有極值0，求實數(shù)
，并確定該極值為極大值還是極小值；
（2）在（1）的條件下，當
時， 
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】《九章算術》中有這樣一則問題：“今有良馬與弩馬發(fā)長安，至齊，齊去長安三千里，良馬初日行一百九十三里，日增一十三里；弩馬初日行九十七里，日減半里，良馬先至齊，復還迎弩馬.”則現(xiàn)有如下說法：
①弩馬第九日走了九十三里路；
②良馬前五日共走了一千零九十五里路；
③良馬和弩馬相遇時，良馬走了二十一日.
則以上說法錯誤的個數(shù)是（ ）個
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com