
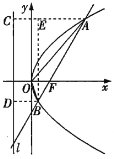
【題目】已知F為拋物線![]() 的焦點,過點F的直線交拋物線于A,B兩點,其中A在x軸上方,O是坐標原點,若
的焦點,過點F的直線交拋物線于A,B兩點,其中A在x軸上方,O是坐標原點,若![]() ,
,![]() ,則以AB為直徑的圓的標準方程為____.
,則以AB為直徑的圓的標準方程為____.
【答案】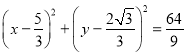
【解析】
解法一:如圖,過點![]() ,
,![]() 分別作拋物線的準線
分別作拋物線的準線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,
,![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,由拋物線的定義算出
,由拋物線的定義算出![]() ,
,![]() ,則可推出
,則可推出
![]() ,又
,又![]() ,得
,得![]() ,從而確定拋物線的解析式及直線
,從而確定拋物線的解析式及直線![]() 的解析式,最后聯立直線
的解析式,最后聯立直線![]() 與拋物線的方程,由根與系數關系及弦長公式求得所求圓的圓心和半徑,進而求出圓的方程;
與拋物線的方程,由根與系數關系及弦長公式求得所求圓的圓心和半徑,進而求出圓的方程;
解法二:如圖,過點![]() 分別作拋物線的準線
分別作拋物線的準線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,由拋物線的定義算出
,由拋物線的定義算出![]() ,
,![]() ,則
,則![]() ,求出直線
,求出直線![]() 的斜率,然后借助點到直線的距離公式及三角形面積公式求得
的斜率,然后借助點到直線的距離公式及三角形面積公式求得![]() 的值,從而確定拋物線的解析式及直線
的值,從而確定拋物線的解析式及直線![]() 的解析式,最后聯立直線
的解析式,最后聯立直線![]() 與拋物線的方程,求得所求圓的圓心和半徑,進而求出圓的方程.
與拋物線的方程,求得所求圓的圓心和半徑,進而求出圓的方程.
解法一:
如圖,過點![]() ,
,![]() 分別作拋物線的準線
分別作拋物線的準線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,
,![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,
,
∵![]() ,∴由拋物線的定義可得
,∴由拋物線的定義可得![]() ,
,
∴![]() ,
,
∵![]() ,
,
又![]() ,
,
∴![]() ,得
,得![]() 易知
易知![]() ,
,
∴直線![]() 的傾斜角為60°,∴直線
的傾斜角為60°,∴直線![]() 的方程為
的方程為![]() ,代入拋物線的方程
,代入拋物線的方程![]() ,得
,得![]() .設
.設![]() ,
,![]() ,則
,則![]() ,
,
∴以![]() 為直徑的圓的標準方程為
為直徑的圓的標準方程為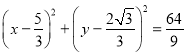 .
.

解法二:
如圖,過點![]() 分別作拋物線的準線
分別作拋物線的準線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,
,
∵![]() ,∴由拋物線的定義可得
,∴由拋物線的定義可得![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴直線![]() 的斜率
的斜率![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
∵原點![]() 到直線
到直線![]() 的距離
的距離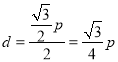 ,且
,且![]() ,
,
∴![]() ,∴直線
,∴直線![]() 的方程為
的方程為![]() ,代入拋物線的方程
,代入拋物線的方程![]() ,
,
得![]() ,
,
設![]() ,則
,則![]() ,
,
∴以![]() 為直徑的圓的標準方程為
為直徑的圓的標準方程為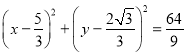 .
.
故答案為: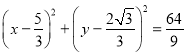


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
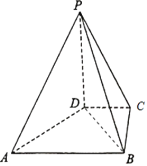
(1)求證:AD⊥PB;
(2)求A點到平面BPC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,各項為正的等比數列
為等差數列,各項為正的等比數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 這三個條件中任選其中一個,補充在橫線上,并完成下面問題的解答(如果選擇多個條件解答,則以選擇第一個解答記分).
這三個條件中任選其中一個,補充在橫線上,并完成下面問題的解答(如果選擇多個條件解答,則以選擇第一個解答記分).
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市實驗中學數學教研組,在高三理科一班進行了一次“采用兩種不同方式進行答卷”的考試實驗,第一種做卷方式:按從前往后的順序依次做;第二種做卷方式:先做簡單題,再做難題.為了比較這兩種做卷方式的效率,選取了![]() 名學生,將他們隨機分成兩組,每組
名學生,將他們隨機分成兩組,每組![]() 人.第一組學生用第一種方式,第二組學生用第二種方式,根據學生的考試分數(單位:分)繪制了莖葉圖如圖所示.
人.第一組學生用第一種方式,第二組學生用第二種方式,根據學生的考試分數(單位:分)繪制了莖葉圖如圖所示.
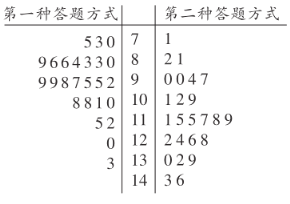
![]() 若
若![]() 分(含
分(含![]() 分)以上為優秀,根據莖葉圖估計兩種做卷方式的優秀率;
分)以上為優秀,根據莖葉圖估計兩種做卷方式的優秀率;
![]() 設
設![]() 名學生考試分數的中位數為
名學生考試分數的中位數為![]() ,根據莖葉圖填寫下面的
,根據莖葉圖填寫下面的![]() 列聯表:
列聯表:
超過中位數 | 不超過中位數 | 合計 | |
第一種做卷方式 | |||
第一種做卷方式 | |||
合計 |
根據列聯表,能否有![]() 的把握認為兩種做卷方式的效率有差異?
的把握認為兩種做卷方式的效率有差異?
附: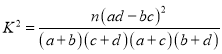 ,
,![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓錐PO中,AB是圓O的直徑,且AB=4,C是底面圓O上一點,且AC=2![]() ,點D為半徑OB的中點,連接PD.
,點D為半徑OB的中點,連接PD.
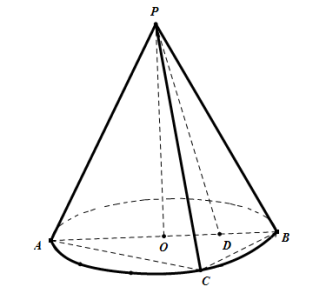
(1)求證:PC在平面APB內的射影是PD;
(2)若PA=4,求底面圓心O到平面PBC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正△ABC邊長為3,點M,N分別是AB,AC邊上的點,AN=BM=1,如圖1所示.將△AMN沿MN折起到△PMN的位置,使線段PC長為![]() ,連接PB,如圖2所示.
,連接PB,如圖2所示.
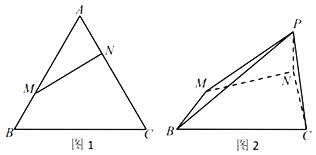
(Ⅰ)求證:平面PMN⊥平面BCNM;
(Ⅱ)若點D在線段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com