
【題目】已知函數 ![]() .
.
(1)討論 ![]() 的單調性;
的單調性;
(2)若 ![]() 有兩個極值點
有兩個極值點 ![]() ,
, ![]() ,證明:
,證明: ![]() .
.
【答案】
(1)解:函數 ![]() 的定義域為
的定義域為 ![]() .
. ![]() .
.![]() ,方程
,方程 ![]() 的判別式
的判別式 ![]() .
.
①當 ![]() 時,
時, ![]() ,∴
,∴ ![]() ,故函數
,故函數 ![]() 在
在 ![]() 上遞減;
上遞減;
②當 ![]() 時,
時, ![]() ,由
,由 ![]() 可得
可得 ![]() ,
, ![]() .
. 
函數 ![]() 的減區間為
的減區間為 ![]() ;增區間為
;增區間為 ![]() .
.
所以,當 ![]() 時,
時, ![]() 在
在 ![]() 上遞減;當
上遞減;當 ![]() 時,
時, ![]() 在
在 ![]() 上遞增,在
上遞增,在 ![]() 上遞減
上遞減
(2)解:由 (1)知當 ![]() 時,函數
時,函數 ![]() 有兩個極值點
有兩個極值點 ![]() ,且
,且 ![]() .
.![]()
![]()
![]()
設 ![]() ,則
,則 ![]() ,
, ![]() ,
,
所以 ![]() 在
在 ![]() 上遞增,
上遞增, ![]() ,
,
所以 ![]() .
.
【解析】(1)根據題目中所給的條件的特點,先求出函數的導數,通過分類討論a的值,確定導函數的符號,利用導數研究函數的單調性,從而判斷函數的單調性;
(2)表示出f(x1)+f(x2),通過利用導數求閉區間上函數的最值進行證明.導數和函數的單調性的關系:
(1)若f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數,f′(x)>0的解集與定義域的交集的對應區間為增區間;
(2)若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數,f′(x)<0的解集與定義域的交集的對應區間為減區間.


科目:高中數學 來源: 題型:
【題目】設有下面四個命題
p1:若復數z滿足 ![]() ∈R,則z∈R;
∈R,則z∈R;
p2:若復數z滿足z2∈R,則z∈R;
p3:若復數z1 , z2滿足z1z2∈R,則z1= ![]() ;
;
p4:若復數z∈R,則 ![]() ∈R.
∈R.
其中的真命題為( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓 ![]() :
: ![]() (
( ![]() )的焦距與橢圓
)的焦距與橢圓 ![]() :
: ![]() 的短軸長相等,且
的短軸長相等,且 ![]() 與
與 ![]() 的長軸長相等,這兩個橢圓在第一象限的交點為
的長軸長相等,這兩個橢圓在第一象限的交點為 ![]() ,直線
,直線 ![]() 經過
經過 ![]() 在
在 ![]() 軸正半軸上的頂點
軸正半軸上的頂點 ![]() 且與直線
且與直線 ![]() (
( ![]() 為坐標原點)垂直,
為坐標原點)垂直, ![]() 與
與 ![]() 的另一個交點為
的另一個交點為 ![]() ,
, ![]() 與
與 ![]() 交于
交于 ![]() ,
, ![]() 兩點.
兩點.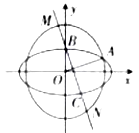
(1)求 ![]() 的標準方程;
的標準方程;
(2)求 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點 ![]() ,焦點在
,焦點在 ![]() 軸上,離心率為
軸上,離心率為 ![]() 的橢圓過點
的橢圓過點 ![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)設橢圓與 ![]() 軸的非負半軸交于點
軸的非負半軸交于點 ![]() ,過點
,過點 ![]() 作互相垂直的兩條直線,分別交橢圓于點
作互相垂直的兩條直線,分別交橢圓于點 ![]() ,
, ![]() 兩點,連接
兩點,連接 ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為半圓
為半圓 ![]() 的直徑,點
的直徑,點 ![]() 是半圓弧上的兩點,
是半圓弧上的兩點, ![]() ,
, ![]() .曲線
.曲線 ![]() 經過點
經過點 ![]() ,且曲線
,且曲線 ![]() 上任意點
上任意點 ![]() 滿足:
滿足: ![]() 為定值.
為定值.
(Ⅰ)求曲線 ![]() 的方程;
的方程;
(Ⅱ)設過點 ![]() 的直線
的直線 ![]() 與曲線
與曲線 ![]() 交于不同的兩點
交于不同的兩點 ![]() ,求
,求 ![]() 面積最大時的直線
面積最大時的直線 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com