【題目】在xOy平面上，將雙曲線的一支
及其漸近線
和直線
、
圍成的封閉圖形記為D，如圖中陰影部分，記D繞y軸旋轉(zhuǎn)一周所得的幾何體為
，過(guò)
作的水平截面，計(jì)算截面面積，利用祖暅原理得出體積為________
【答案】
.
【解析】分析：由已知中過(guò)（0，y）（0≤y≤4）作Ω的水平截面，計(jì)算截面面積，利用祖暅原理得出Ω的體積．
詳解：在xOy平面上，將雙曲線的一支
及其漸近線
和直線y=0，y=4圍成的封閉圖形記為D，如圖中陰影部分．
則直線y=a與漸近線交于一點(diǎn)A（
，a）點(diǎn)，與雙曲線的一支 交于B（
，a）點(diǎn)，
記D繞y軸旋轉(zhuǎn)一周所得的幾何體為Ω．
過(guò)（0，y）（0≤y≤4）作Ω的水平截面，
則截面面積S=
，
利用祖暅原理得Ω的體積相當(dāng)于底面面積為9π高為4的圓柱的體積，
∴Ω的體積V=9π×4=36π，
故答案為：36π
學(xué)業(yè)測(cè)評(píng)一課一測(cè)系列答案
小學(xué)課時(shí)作業(yè)全通練案系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知函數(shù)
.
(1)當(dāng)
時(shí),討論
的單調(diào)性；
(2)設(shè)
，當(dāng)
時(shí),若對(duì)任意
,存在
使
,求實(shí)數(shù)
取值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分） 
（1）證明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在多面體
中，平面
平面
，四邊形
為正方形，四邊形為梯形，且
，
，
．
（Ⅰ）求證：
平面
；
（Ⅱ）求證：
平面
；
（Ⅲ）在線段
上是否存在點(diǎn)
，使得
平面
？若存在，求出
的值；若不存在，請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，PA⊥底面ABC，∠BAC=90°．點(diǎn)D，E，N分別為棱PA，PC，BC的中點(diǎn)，M是線段AD的中點(diǎn)，PA=AC=4，AB=2．
（Ⅰ）求證：MN∥平面BDE；
（Ⅱ）求二面角C﹣EM﹣N的正弦值；
（Ⅲ）已知點(diǎn)H在棱PA上，且直線NH與直線BE所成角的余弦值為 
，求線段AH的長(zhǎng)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】現(xiàn)在，很多人都喜歡騎“共享單車(chē)”，但也有很多市民并不認(rèn)可．為了調(diào)查人們對(duì)這種交通方式的認(rèn)可度，某同學(xué)從交通擁堵不嚴(yán)重的A城市和交通擁堵嚴(yán)重的B城市分別隨機(jī)調(diào)查了20名市民，得到了一個(gè)市民是否認(rèn)可的樣本，具體數(shù)據(jù)如下
列聯(lián)表：
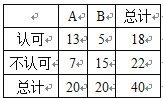
附：
，
．
根據(jù)表中的數(shù)據(jù)，下列說(shuō)法中，正確的是（ ）
A. 沒(méi)有95% 以上的把握認(rèn)為“是否認(rèn)可與城市的擁堵情況有關(guān)”
B. 有99% 以上的把握認(rèn)為“是否認(rèn)可與城市的擁堵情況有關(guān)”
C. 可以在犯錯(cuò)誤的概率不超過(guò)0.01的前提下認(rèn)為“是否認(rèn)可與城市的擁堵情況有關(guān)”
D. 可以在犯錯(cuò)誤的概率不超過(guò)0.025的前提下認(rèn)為“是否認(rèn)可與城市的擁堵情況有關(guān)”
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在平面直角坐標(biāo)系
中，已知直線
的參數(shù)方程為
（
為參數(shù)）.以坐標(biāo)原點(diǎn)
為極點(diǎn)，以坐標(biāo)原點(diǎn)為極點(diǎn)，
軸的非負(fù)半軸為極軸，取相同的長(zhǎng)度單位建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
.
(Ⅰ)求直線的普通方程和曲線的直角坐標(biāo)方程；
(Ⅱ)若曲線上的點(diǎn)到直線的最大距離為6，求實(shí)數(shù)
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在四棱錐
中，底面
是菱形，對(duì)角線
，
交于點(diǎn)
．
（Ⅰ）若
，求證：
平面
；
（Ⅱ）若平面
平面，求證：
；
（Ⅲ）在棱
上是否存在點(diǎn)
（異于點(diǎn)
），使得
平面
？說(shuō)明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某研究機(jī)構(gòu)對(duì)高三學(xué)生的記憶力
和判斷力
進(jìn)行統(tǒng)計(jì)分析，得下表數(shù)據(jù)：
（1）請(qǐng)根據(jù)上表提供的數(shù)據(jù)，用相關(guān)系數(shù)
說(shuō)明與的線性相關(guān)程度；（結(jié)果保留小數(shù)點(diǎn)后兩位，參考數(shù)據(jù): 
）
（2）請(qǐng)根據(jù)上表提供的數(shù)據(jù)，用最小二乘法求出
關(guān)于
的線性回歸方程
；
（3）試根據(jù)求出的線性回歸方程，預(yù)測(cè)記憶力為9的同學(xué)的判斷力．
參考公式：
，
；相關(guān)系數(shù)
；
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com