
【題目】已知動圓過定點A(4,0),且在y軸上截得的弦MN的長為8.
(1)求動圓圓心的軌跡C的方程;
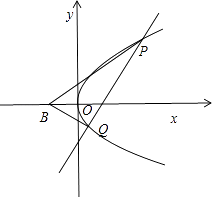
(2)已知點B(﹣1,0),設不垂直于x軸的直線與軌跡C交于不同的兩點P,Q,若x軸是∠PBQ的角平分線,證明直線過定點.
【答案】
(1)解:設圓心C(x,y)(x≠0),過點C作CE⊥y 軸,垂足為E,則|ME|= ![]() |MN|,
|MN|,
∴|CA|2=|CM|2=|ME|2+|EC|2,
∴(x﹣4)2+y2=42+x2,化為y2=8x.
當x=0時,也滿足上式.
∴動圓圓心的軌跡C的方程為y2=8x.
(2)解:設P(x1,y1),Q(x2,y2),
由題意可知y1+y2≠0,y1y2<0. ![]() ,
, ![]() .
.
∵x軸是∠PBQ的角平分線,∴kPB=﹣kQB,
∴ ![]() ,∴
,∴ 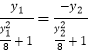 ,化為8+y1y2=0.
,化為8+y1y2=0.
直線PQ的方程為 ![]() ,
,
∴ 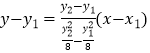 ,化為
,化為 ![]() ,
,
化為 ![]() ,
,
y(y1+y2)+8=8x,令y=0,則x=1,
∴直線PQ過 定點(1,0)
【解析】(1)設圓心C(x,y),過點C作CE⊥y 軸,垂足為E,利用垂徑定理可得|ME|= ![]() |MN|,又|CA|2=|CM|2=|ME|2+|EC|2 , 利用兩點間的距離公式即可得出.(2)設P(x1 , y1),Q(x2 , y2),由題意可知y1+y2≠0,y1y2<0.
|MN|,又|CA|2=|CM|2=|ME|2+|EC|2 , 利用兩點間的距離公式即可得出.(2)設P(x1 , y1),Q(x2 , y2),由題意可知y1+y2≠0,y1y2<0. ![]() ,
, ![]() .利用角平分線的性質可得kPB=﹣kQB , 可化為化為8+y1y2=0.又直線PQ的方程為
.利用角平分線的性質可得kPB=﹣kQB , 可化為化為8+y1y2=0.又直線PQ的方程為 ![]() ,代入化簡整理為y(y1+y2)+8=8x,令y=0,則x=1即可得到定點.
,代入化簡整理為y(y1+y2)+8=8x,令y=0,則x=1即可得到定點.


科目:高中數學 來源: 題型:
【題目】已知某中學高三文科班學生共有800人參加了數學與地理的水平測試,學校決定利用隨機數表法從中抽取100人進行成績抽樣調查,先將800人按001,002,…,800進行編號.
(1)如果從第8行第7列的數開始向右讀,請你依次寫出最先檢查的3個人的編號;
(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的數學與地理的水平測試成績如下表:
成績分為優秀、良好、及格三個等級;橫向,縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42.
人數 | 數學 | |||
優秀 | 良好 | 及格 | ||
| 優秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
①若在該樣本中,數學成績優秀率是30%,求a,b的值:
②在地理成績及格的學生中,已知![]() 求數學成績優秀的人數比及格的人數少的概率.
求數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了安排生產任務,需要確定加工零件所花費的時間,為此作了四次試 驗,得到的數據如下:
零件的個數x(件) |
|
|
|
|
加工的時間y(小時) |
|
|
|
|
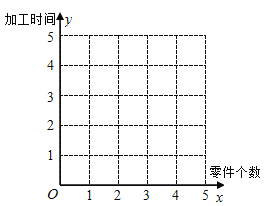
(1)在給定的坐標系中畫出表中數據的散點圖;
(2)求出y關于x的線性回歸方程![]() ,并在坐標系中畫出回歸直線;
,并在坐標系中畫出回歸直線;
(3)試預測生產10個零件需要多少時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據說偉大的阿基米德逝世后,敵軍將領馬塞拉斯給他建了一塊墓碑,在墓碑上刻了一個如圖所示的圖案,圖案中球的直徑、圓柱底面的直徑和圓柱的高相等,圓錐的頂點為圓柱上底面的圓心,圓錐的底面是圓柱的下底面.
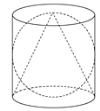
(1)試計算出圖案中球與圓柱的體積比;
(2)假設球半徑![]() .試計算出圖案中圓錐的體積和表面積.
.試計算出圖案中圓錐的體積和表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如圖.

(1)求分數在![]() 的頻數及全班人數;
的頻數及全班人數;
(2)求分數在![]() 之間的頻數,并計算頻率分布直方圖中
之間的頻數,并計算頻率分布直方圖中![]() 間矩形的高.
間矩形的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為招聘新員工設計了一個面試方案:應聘者從![]() 道備選題中一次性隨機抽取
道備選題中一次性隨機抽取![]() 道題,按照題目要求獨立完成規定:至少正確完成其中
道題,按照題目要求獨立完成規定:至少正確完成其中![]() 道題的便可通過.已知
道題的便可通過.已知![]() 道備選題中應聘者甲有
道備選題中應聘者甲有![]() 道題能正確完成,
道題能正確完成,![]() 道題不能完成;應聘者乙每題正確完成的概率都是
道題不能完成;應聘者乙每題正確完成的概率都是![]() ,且每題正確完成與否互不影響
,且每題正確完成與否互不影響
(1)分別求甲、乙兩人正確完成面試題數的分布列,并計算其數學期望;
(2)請分析比較甲、乙兩人誰的面試通過的可能性大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩支排球隊進行比賽,先勝3局者獲得比賽的勝利,比賽隨即結束.除第五局甲隊獲勝的概率是 ![]() ,其余每局比賽甲隊獲勝的概率都是
,其余每局比賽甲隊獲勝的概率都是 ![]() .設各局比賽結果相互獨立.
.設各局比賽結果相互獨立.
(1)分別求甲隊3:0,3:1,3:2勝利的概率;
(2)若比賽結果3:0或3:1,則勝利方得3分,對方得0分;若比賽結果為3:2,則勝利方得2分,對方得1分,求乙隊得分X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,已知四邊形BCDE為直角梯形,![]() ,
,![]() ,且
,且![]() ,A為BE的中點
,A為BE的中點![]() 將
將![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如圖
如圖![]() ,連結PC,PB構成一個四棱錐
,連結PC,PB構成一個四棱錐![]() .
.

![]() Ⅰ
Ⅰ![]() 求證
求證![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在點M,滿足
在棱PC上存在點M,滿足![]() ,使得直線AM與平面PBC所成的角為
,使得直線AM與平面PBC所成的角為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com