
【題目】已知函數(shù)![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)證明:![]() .
.
【答案】(1)當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;當(dāng)
上單調(diào)遞增;當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;(2)證明見解析.
上單調(diào)遞減;(2)證明見解析.
【解析】
(1)求導(dǎo)后分![]() 與
與![]() 兩種情況分析導(dǎo)數(shù)的正負(fù)從而求得原函數(shù)的單調(diào)性即可.
兩種情況分析導(dǎo)數(shù)的正負(fù)從而求得原函數(shù)的單調(diào)性即可.
(2)根據(jù)(1)中的結(jié)論,求得![]() 最小值從而得出當(dāng)
最小值從而得出當(dāng)![]() 時,
時,![]() ,再構(gòu)造函數(shù)式證明
,再構(gòu)造函數(shù)式證明![]() .或構(gòu)造
.或構(gòu)造![]() ,求導(dǎo)后根據(jù)隱零點(diǎn)的方法證明.
,求導(dǎo)后根據(jù)隱零點(diǎn)的方法證明.
(1)依題意,![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() .
.
①當(dāng)![]() 時,若
時,若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
②當(dāng)![]() 時,若
時,若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
綜上,當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(2)法一:由(1)知,當(dāng)![]() 時,
時,![]() ,在
,在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,所以
上單調(diào)遞減,所以![]() ,
,
故當(dāng)![]() 時,
時,![]() .
.
又當(dāng)![]() 時,
時,![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,故
,故![]() ,
,
所以![]() .
.
(2)法二:令![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() 為增函數(shù),且
為增函數(shù),且
![]() ,
,![]() ,
,
所以![]() 有唯一的零點(diǎn)
有唯一的零點(diǎn)![]() ,
,![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,
,![]() 為減函數(shù);當(dāng)
為減函數(shù);當(dāng)![]() 時,
時,![]() 為增函數(shù).
為增函數(shù).
所以![]() .
.
由(1)知,當(dāng)![]() 時,
時,![]() 在
在![]() 上為減函數(shù),在
上為減函數(shù),在![]() 上為增函數(shù),故
上為增函數(shù),故
![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,故
,故![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,底面
中,底面![]() 是邊長為4的等邊三角形,
是邊長為4的等邊三角形,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)證明:![]() 平面
平面![]() .
.
(2)若![]() 是等邊三角形,求二面角
是等邊三角形,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 為常數(shù),
為常數(shù),![]() )的圖象關(guān)于直線
)的圖象關(guān)于直線![]() 對稱,則函數(shù)
對稱,則函數(shù)![]() 的圖象( )
的圖象( )
A. 關(guān)于直線![]() 對稱B. 關(guān)于直線
對稱B. 關(guān)于直線![]() 對稱
對稱
C. 關(guān)于點(diǎn)![]() 對稱D. 關(guān)于點(diǎn)
對稱D. 關(guān)于點(diǎn)![]() 對稱
對稱
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知兩定點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是平面內(nèi)的動點(diǎn),且
是平面內(nèi)的動點(diǎn),且![]() ,記
,記![]() 的軌跡是
的軌跡是![]()
(1)求曲線![]() 的方程;
的方程;
(2)過點(diǎn)![]() 引直線
引直線![]() 交曲線
交曲線![]() 于
于![]() 兩點(diǎn),設(shè)
兩點(diǎn),設(shè)![]() ,點(diǎn)
,點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對稱點(diǎn)為
軸的對稱點(diǎn)為![]() ,證明直線
,證明直線![]() 過定點(diǎn).
過定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某紡織廠為了生產(chǎn)一種高端布料,準(zhǔn)備從![]() 農(nóng)場購進(jìn)一批優(yōu)質(zhì)棉花,廠方技術(shù)人員從
農(nóng)場購進(jìn)一批優(yōu)質(zhì)棉花,廠方技術(shù)人員從![]() 農(nóng)場存儲的優(yōu)質(zhì)棉花中隨機(jī)抽取了
農(nóng)場存儲的優(yōu)質(zhì)棉花中隨機(jī)抽取了![]() 處棉花,分別測量了其纖維長度(單位:
處棉花,分別測量了其纖維長度(單位:![]() )的均值,收集到
)的均值,收集到![]() 個樣本數(shù)據(jù),并制成如下頻數(shù)分布表:
個樣本數(shù)據(jù),并制成如下頻數(shù)分布表:

(1)求這![]() 個樣本數(shù)據(jù)的平均數(shù)和樣本方差(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表);
個樣本數(shù)據(jù)的平均數(shù)和樣本方差(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表);
(2)將收集到的數(shù)據(jù)繪制成直方圖可以認(rèn)為這批棉花的纖維長度服從分布![]() ,其中
,其中![]() .
.
①利用正態(tài)分布,求![]() ;
;
②紡織廠將![]() 農(nóng)場送來的這批優(yōu)質(zhì)棉進(jìn)行二次檢驗,從中隨機(jī)抽取
農(nóng)場送來的這批優(yōu)質(zhì)棉進(jìn)行二次檢驗,從中隨機(jī)抽取![]() 處測量其纖維均值
處測量其纖維均值![]() ,數(shù)據(jù)如下:
,數(shù)據(jù)如下:

若![]() 個樣本中纖維均值
個樣本中纖維均值![]() 的頻率不低于①中
的頻率不低于①中![]() ,即可判斷該批優(yōu)質(zhì)棉花合格,否則認(rèn)為農(nóng)場運(yùn)送是摻雜了次品,判斷該批棉花不合格.按照此依據(jù)判斷
,即可判斷該批優(yōu)質(zhì)棉花合格,否則認(rèn)為農(nóng)場運(yùn)送是摻雜了次品,判斷該批棉花不合格.按照此依據(jù)判斷![]() 農(nóng)場送來的這批棉花是否為合格的優(yōu)質(zhì)棉花,并說明理由.
農(nóng)場送來的這批棉花是否為合格的優(yōu)質(zhì)棉花,并說明理由.
附:若![]() ,則
,則![]()
![]()
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某林場現(xiàn)有木材存量為![]() ,每年以25%的增長率逐年遞增,但每年年底要砍伐的木材量為
,每年以25%的增長率逐年遞增,但每年年底要砍伐的木材量為![]() ,經(jīng)過
,經(jīng)過![]() 年后林場木材存有量為
年后林場木材存有量為![]()
(1)求![]() 的解析式
的解析式
(2)為保護(hù)生態(tài)環(huán)境,防止水土流失,該地區(qū)每年的森林木材存量不應(yīng)少于![]() ,如果
,如果![]() ,那么該地區(qū)會發(fā)生水土流失嗎?若會,要經(jīng)過幾年?(取
,那么該地區(qū)會發(fā)生水土流失嗎?若會,要經(jīng)過幾年?(取![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為側(cè)棱
為側(cè)棱![]() 上一點(diǎn).
上一點(diǎn).
(Ⅰ)若![]() ,求證:
,求證:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)在側(cè)棱![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出線段
?若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了進(jìn)一步推動全市學(xué)習(xí)型黨組織、學(xué)習(xí)型社會建設(shè),某市組織開展“學(xué)習(xí)強(qiáng)國”知識測試,每人測試文化、經(jīng)濟(jì)兩個項目,每個項目滿分均為60分.從全體測試人員中隨機(jī)抽取了100人,分別統(tǒng)計他們文化、經(jīng)濟(jì)兩個項目的測試成績,得到文化項目測試成績的頻數(shù)分布表和經(jīng)濟(jì)項目測試成績的頻率分布直方圖如下:
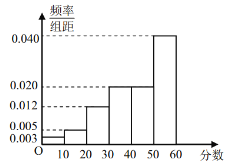
經(jīng)濟(jì)項目測試成績頻率分布直方圖
分?jǐn)?shù)區(qū)間 | 頻數(shù) |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化項目測試成績頻數(shù)分布表
將測試人員的成績劃分為三個等級如下:分?jǐn)?shù)在區(qū)間![]() 內(nèi)為一般,分?jǐn)?shù)在區(qū)間
內(nèi)為一般,分?jǐn)?shù)在區(qū)間![]() 內(nèi)為良好,分?jǐn)?shù)在區(qū)間
內(nèi)為良好,分?jǐn)?shù)在區(qū)間![]() 內(nèi)為優(yōu)秀.
內(nèi)為優(yōu)秀.
(1)在抽取的100人中,經(jīng)濟(jì)項目等級為優(yōu)秀的測試人員中女生有14人,經(jīng)濟(jì)項目等級為一般或良好的測試人員中女生有34人.填寫下面列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有![]() 以上的把握認(rèn)為“經(jīng)濟(jì)項目等級為優(yōu)秀”與性別有關(guān)?
以上的把握認(rèn)為“經(jīng)濟(jì)項目等級為優(yōu)秀”與性別有關(guān)?
優(yōu)秀 | 一般或良好 | 合計 | |
男生數(shù) | |||
女生數(shù) | |||
合計 |
(2)用這100人的樣本估計總體,假設(shè)這兩個項目的測試成績相互獨(dú)立.
(i)從該市測試人員中隨機(jī)抽取1人,估計其“文化項目等級高于經(jīng)濟(jì)項目等級”的概率.
(ii)對該市文化項目、經(jīng)濟(jì)項目的學(xué)習(xí)成績進(jìn)行評價.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在長方體![]() 中,
中,![]() ,點(diǎn)E是棱
,點(diǎn)E是棱![]() 上的一個動點(diǎn),若平面
上的一個動點(diǎn),若平面![]() 交棱
交棱![]() 于點(diǎn)
于點(diǎn)![]() ,給出下列命題:
,給出下列命題:
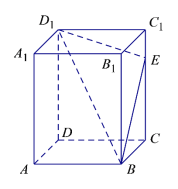
①四棱錐![]() 的體積恒為定值;
的體積恒為定值;
②存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ;
;
③對于棱![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,在棱
,在棱![]() 上均有相應(yīng)的點(diǎn)
上均有相應(yīng)的點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的點(diǎn)![]() ,使得截面四邊形
,使得截面四邊形![]() 的周長取得最小值.
的周長取得最小值.
其中真命題的是____________.(填寫所有正確答案的序號)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com