【題目】在銳角三角形ABC中，9tanAtanB+tanBtanC+tanCtanA的最小值為 ．
【答案】25
【解析】解：如圖，不妨設CD=1，AD=m，BD=n，
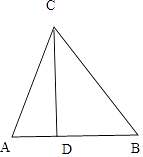
∴tanA= 
，tanB= 
，（m＞0，n＞0），
∴tanC=
tan（A+B）= 
= 
，
∵tanC＞0，
∴mn＜1，
∴9tanAtanB+tanBtanC+tanCtanA= 
+（ + ） ，
= + 
，
≥ + 
，
=（ + ）[mn+（1﹣mn）]，
=9+4+ 
+ 
，
≥13+2 
=13+12=25，當且僅當 = ，即m=n= 
時取等號，
故最小值為25，
所以答案是：25 .
【考點精析】本題主要考查了基本不等式在最值問題中的應用的相關知識點，需要掌握用基本不等式求最值時（積定和最小，和定積最大），要注意滿足三個條件“一正、二定、三相等”才能正確解答此題．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】設△ABC的三個內角分別為A，B，C．向量 
共線． （Ⅰ）求角C的大小；
（Ⅱ）設角A，B，C的對邊分別是a，b，c，且滿足2acosC+c=2b，試判斷△ABC的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=（a2﹣3a+3）ax是指數函數，
（1）求f（x）的表達式；
（2）判斷F（x）=f（x）﹣f（﹣x）的奇偶性，并加以證明
（3）解不等式：loga（1﹣x）＞loga（x+2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于給定的正整數k，如果各項均為正數的數列{an}滿足：對任意正整數n（n＞k），an﹣kan﹣k+1…an﹣1an+1…an+k﹣1an+k=an2k總成立，那么稱{an}是“Q（k）數列”．
（1）若{an}是各項均為正數的等比數列，判斷{an}是否為“Q（2）數列”，并說明理由；
（2）若{an}既是“Q（2）數列”，又是“Q（3）數列”，求證：{an}是等比數列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖為函數y=f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）圖象的一部分，其中點 
是圖象的一個最高點，點 
是與點P相鄰的圖象與x軸的一個交點．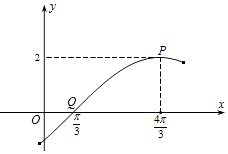
（1）求函數f（x）的解析式；
（2）若將函數f（x）的圖象沿x軸向右平移 
個單位，再把所得圖象上每一點的橫坐標都變為原來的 
（縱坐標不變），得到函數y=g（x）的圖象，求函數y=g（x）的單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐 
中，底面 
是菱形， 
， 
平面 ， 
， 
， 
， 
是 
中點．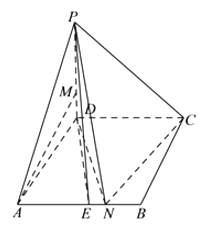
（I）求證：直線 
平面 
．
（II）求證：直線 
平面 
．
（III）在 上是否存在一點 
，使得二面角 
的大小為 
，若存在，確定 的位置，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
﹣ 
+cx+d有極值．
（Ⅰ）求實數c的取值范圍；
（Ⅱ）若f（x）在x=2處取得極值，且當x＜0時，f（x）＜ 
+2d恒成立，求實數d的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
