
【題目】已知函數![]()
![]() 是
是![]() 的一個極值點.
的一個極值點.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若當![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)單調增區間為(﹣∞,1),(2,+∞);單調減區間為(1,2).(2)0<a<1.
【解析】
(1)求導函數,利用f'(2),可求b的值,進而利用f'(x)>0可得函數f(x)的單調增區間,f'(x)<0可得函數f(x)的單調減區間;
(2)x∈[1,+∞)時,![]() 恒成立等價于
恒成立等價于![]() ,由此可求a的取值范圍.
,由此可求a的取值范圍.
(1)求導函數,可得f'(x)=x2﹣2bx+2
∵x=2是f(x)的一個極值點
∴f'(2)=4﹣4b+2=0,∴![]() ,∴f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
,∴f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
由f'(x)>0得x>2或x<1,∴函數f(x)的單調增區間為(﹣∞,1),(2,+∞);
由f'(x)<0得1<x<2,∴函數f(x)的單調減區間為(1,2).
(2)由(1)知,函數f(x)在(1,2)上單調遞減,在(2,+∞)上單調遞增
∴當x=2時,函數f(x)取得最小值,f(x)min=f(2)![]() ,
,
x∈[1,+∞)時,![]() 恒成立等價于
恒成立等價于![]()
即a2﹣a<0,
∴0<a<1.


科目:高中數學 來源: 題型:
【題目】在三棱拄![]() 中,
中,![]() 側面
側面![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)試在棱![]() (不包含端點
(不包含端點![]() )上確定一點
)上確定一點![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,求![]() 和平面
和平面![]() 所成角正弦值的大小.
所成角正弦值的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某兩名高三學生在連續9次數學測試中的成績(單位:分)進行統計得到如下折線圖。下面關于這兩位同學的數學成績的分析中,正確的共有( )個。

①甲同學的成績折線圖具有較好的對稱性,與正態曲線相近,故而平均成績為130分;
②根據甲同學成績折線圖提供的數據進行統計,估計該同學平均成績在區間![]() 內;
內;
③乙同學的數學成績與考試次號具有比較明顯的線性相關性,且為正相關;
④乙同學在這連續九次測驗中的最高分與最低分的差超過40分。
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
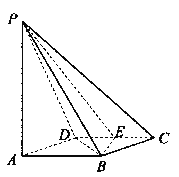
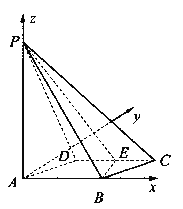
【題目】如圖所示,四棱錐![]() 的底面
的底面![]() 是邊長為1的菱形,
是邊長為1的菱形,![]() ,
,
E是CD的中點,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)證明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.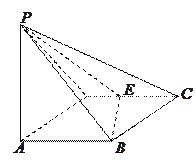
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列對各事件發生的概率判斷正確的是( )
A.某學生在上學的路上要經過4個路口,假設在各路口是否遇到紅燈是相互獨立的,遇到紅燈的概率都是![]() ,那么該生在上學路上到第3個路口首次遇到紅燈的概率為
,那么該生在上學路上到第3個路口首次遇到紅燈的概率為![]()
B.三人獨立地破譯一份密碼,他們能單獨譯出的概率分別為![]() ,
,![]() ,
,![]() ,假設他們破譯密碼是彼此獨立的,則此密碼被破譯的概率為
,假設他們破譯密碼是彼此獨立的,則此密碼被破譯的概率為![]()
C.甲袋中有8個白球,4個紅球,乙袋中有6個白球,6個紅球,從每袋中各任取一個球,則取到同色球的概率為![]()
D.設兩個獨立事件A和B都不發生的概率為![]() ,A發生B不發生的概率與B發生A不發生的概率相同,則事件A發生的概率是
,A發生B不發生的概率與B發生A不發生的概率相同,則事件A發生的概率是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市由甲、乙兩家乒乓球俱樂部,兩家設備和服務都很好,但收費方式不同,甲家每張球臺每小時5元;乙家按月計費,一個月中30小時以內(含30小時)每張球臺90元,超過30小時的部分每張球臺每小時2元.某公司準備下個月從兩家中的一家租一張球臺開展活動,活動時間不少于15小時,也不超過40小時,設在甲家租一張球臺開展活動![]() 小時的收費為
小時的收費為![]() 元,在乙家租一張球臺開展活動
元,在乙家租一張球臺開展活動![]() 小時的收費為
小時的收費為![]() 元.
元.
(1)寫出![]() 與
與![]() 的解析式;
的解析式;
(2)選擇哪家比較合算?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一張長為80cm、寬為60cm的長方形鐵皮ABCD,準備用它做成一只無蓋長方體鐵皮盒,要求材料利用率為100%,不考慮焊接處損失.如圖,若長方形ABCD的一個角剪下一塊正方形鐵皮,作為鐵皮盒的底面,用余下材料剪拼后作為鐵皮盒的側面,設長方體的底面正方形邊長為x(cm),高為y(cm),體積為V(cm3).求:
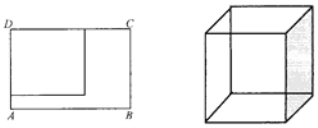
(1)y關于x的表達式;
(2)該鐵皮盒體積V的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車駕駛學校在學員結業前,對學員的駕駛技術進行4次考核,規定:按順序考核,一旦考核合格就不必參加以后的考核,否則還需參加下次考核。若學員小李獨立參加每次考核合格的概率依次組成一個公差為![]() 的等差數列,他參加第一次考核合格的概率不超過
的等差數列,他參加第一次考核合格的概率不超過![]() ,且他直到參加第二次考核才合格的概率為
,且他直到參加第二次考核才合格的概率為![]() .
.
(1)求小李第一次參加考核就合格的概率![]() ;
;
(2)求小李參加考核的次數![]() 的分布列和數學期望
的分布列和數學期望
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com