【題目】已知定義在R上的函數
滿足以下三個條件：①對于任意的
，都有
；②對于任意的
都有
③函數
的圖象關于y軸對稱，則下列結論中正確的是( )
A. 
B. 
C. 
D. 
【答案】B
【解析】
由①可知函數f（x）是周期T=4的周期函數； 由②可得函數f（x）在[0，2]上單調遞增；由③可得函數f（x）的圖象關于直線x=2對稱．于是f（4.5）=f（0.5），f（7）=f（3）=f（1），f（6.5）=f（2.5）=f（1.5）．即可得出結果.
定義在R上的函數y=f（x）滿足以下三個條件：由①對于任意的x∈R，都有f（x+4）=f（x），可知函數f（x）是周期T=4的周期函數； ②對于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2），可得函數f（x）在[0，2]上單調遞增；③函數y=f（x+2）的圖象關于y軸對稱，可得函數f（x）的圖象關于直線x=2對稱．∴f（4.5）=f（0.5），f（7）=f（3）=f（1），f（6.5）=f（2.5）=f（1.5）．∵f（0.5）＜f（1）＜f（1.5），∴f （4.5）＜f （7）＜f （6.5）．
故選：B．
黃岡天天練口算題卡系列答案科目：高中數學 來源： 題型：
【題目】“開門大吉”是某電視臺推出的游戲節目，選手面對1～8號8扇大門，依次按響門上的門鈴，門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹)，選手需正確回答出這首歌的名字，方可獲得該扇門對應的家庭夢想基金.在一次場外調查中，發現參賽選手多數分為兩個年齡段：20～30；30～40(單位：歲).其猜對歌曲名稱與否的人數如圖所示.
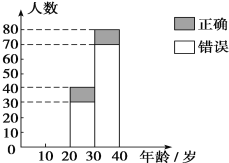
（1）寫出2×2列聯表；判斷能否在犯錯誤的概率不超過0.10的前提下認為猜對歌曲名稱與年齡有關系，說明你的理由.(下面的臨界值表供參考)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（2）現計劃在這次場外調查中按年齡段用分層抽樣的方法選取6名選手，求20～30歲與30～40歲各有幾人.
參考公式：K2＝
，其中n＝a＋b＋c＋d.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解某市高中學生的漢字書寫水平，在全市范圍內隨機抽取了近千名學生參加漢字聽寫考試，將所得數據進行分組，分組區間為：
，并繪制出頻率分布直方圖，如圖所示.
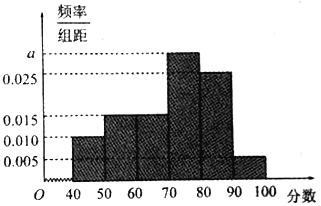
（1）求頻率分布直方圖中
的值，并估計該市高中學生的平均成績；
（2）設
、
、
、
四名學生的考試成績在區間
內，
、
兩名學生的考試成績在區間
內，現從這6名學生中任選兩人參加座談會，求學生、至少有一人被選中的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分14分）已知過原點的動直線
與圓
相交于不同的兩點
，
．
（1）求圓
的圓心坐標；
（2）求線段
的中點
的軌跡
的方程；
（3）是否存在實數
，使得直線
與曲線只有一個交點？若存在，求出的取值范圍；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
（
為參數，實數
），曲線
（為參數，實數
）.在以
為極點，
軸的正半軸為極軸的極坐標系中，射線
與
交于，
兩點，與
交于，
兩點.當
時，
；當
，
.
（1）求
和
的值.
（2）求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A.離散型隨機變量
的方差
反映了隨機變量取值的波動情況；
B.隨機變量
，其中
越小，曲線越“矮胖”；
C.若
與
是相互獨立事件，則與
也是相互獨立事件；
D.從10個紅球和20個白球除顏色外完全相同中，一次摸出5個球，則摸到紅球的個數服從超幾何分布；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．
（Ⅰ）若直線PB與CD所成角的大小為
，求BC的長；
（Ⅱ）求二面角B－PD－A的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
