
【題目】已知定義在R上的偶函數(shù)f(x),其導函數(shù)![]() ,當x≥0時,恒有
,當x≥0時,恒有![]()
![]() +f(﹣x)<0,若g(x)=x2f(x),則不等式g(x)<g(1﹣2x)的解集為( )
+f(﹣x)<0,若g(x)=x2f(x),則不等式g(x)<g(1﹣2x)的解集為( )
A.(![]() ,1)B.(﹣∞,
,1)B.(﹣∞,![]() )∪(1,+∞)
)∪(1,+∞)
C.(![]() ,+∞)D.(﹣∞,
,+∞)D.(﹣∞,![]() )
)
【答案】A
【解析】
根據(jù)函數(shù)f(x)為偶函數(shù),則函數(shù)g(x)也是偶函數(shù),利用導數(shù)判斷函數(shù)![]() 在[0,+∞)上的單調性,則不等式g(x)<g(1﹣2x)等價于g(|x|)<g(|1﹣2x|),解不等式即可.
在[0,+∞)上的單調性,則不等式g(x)<g(1﹣2x)等價于g(|x|)<g(|1﹣2x|),解不等式即可.
因為g(x)=x2f(x),當x≥0時,g′(x)=2x[![]()
![]() +f(﹣x)]≤0,
+f(﹣x)]≤0,
∴函數(shù)g(x)在[0,+∞)上單調遞減.
∵函數(shù)f(x)是定義在R上的偶函數(shù),
∴函數(shù)g(x)是定義在R上的偶函數(shù),
則不等式g(x)<g(1﹣2x)即g(|x|)<g(|1﹣2x|),
∴|x|>|1﹣2x|,解得:![]() <x<1.
<x<1.
∴不等式g(x)<g(1﹣2x)的解集為(![]() ,1).
,1).
故選:A


科目:高中數(shù)學 來源: 題型:
【題目】對于定義域為D的函數(shù)y=f(x),如果存在區(qū)間[m,n]![]() D,同時滿足:
D,同時滿足:
①f(x)在[m,n]內是單調函數(shù);
②當定義域是[m,n]時,f(x)的值域也是[m,n].則稱[m,n]是該函數(shù)的“和諧區(qū)間”.
(1)證明:[0,1]是函數(shù)y=f(x)=x2的一個“和諧區(qū)間”.
(2)求證:函數(shù)![]() 不存在“和諧區(qū)間”.
不存在“和諧區(qū)間”.
(3)已知:函數(shù)![]() (a∈R,a≠0)有“和諧區(qū)間”[m,n],當a變化時,求出n﹣m的最大值.
(a∈R,a≠0)有“和諧區(qū)間”[m,n],當a變化時,求出n﹣m的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖給出的是2000年至2016年我國實際利用外資情況,以下結論正確的是( )
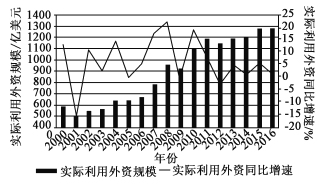
A. 2000年以來我國實際利用外資規(guī)模與年份呈負相關
B. 2010年以來我國實際利用外資規(guī)模逐年增大
C. 2008年以來我國實際利用外資同比增速最大
D. 2010年以來我國實際利用外資同比增速最大
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】南充高中扎實推進陽光體育運動,積極引導學生走向操場,走進大自然,參加體育鍛煉,每天上午第三節(jié)課后全校大課間活動時長35分鐘.現(xiàn)為了了解學生的體育鍛煉時間,采用簡單隨機抽樣法抽取了100名學生,對其平均每日參加體育鍛煉的時間(單位:分鐘)進行調查,按平均每日體育鍛煉時間分組統(tǒng)計如下表:
分組 |
|
|
|
|
|
|
男生人數(shù) | 2 | 16 | 19 | 18 | 5 | 3 |
女生人數(shù) | 3 | 20 | 10 | 2 | 1 | 1 |
若將平均每日參加體育鍛煉的時間不低于120分鐘的學生稱為“鍛煉達人”.
(1)將頻率視為概率,估計我校7000名學生中“鍛煉達人”有多少?
(2)從這100名學生的“鍛煉達人”中按性別分層抽取5人參加某項體育活動.
①求男生和女生各抽取了多少人;
②若從這5人中隨機抽取2人作為組長候選人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小李從網(wǎng)上購買了一件商品,快遞員計劃在下午5:00-6:00之間送貨上門,已知小李下班到家的時間為下午5:30-6:00.快遞員到小李家時,如果小李未到家,則快遞員會電話聯(lián)系小李.若小李能在10分鐘之內到家,則快遞員等小李回來;否則,就將商品存放在快遞柜中.則小李需要去快遞柜收取商品的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() ,
,![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的坐標方程為
的坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切.
相切.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() 、
、![]() 于原點
于原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知首項相等的兩個數(shù)列![]() 滿足
滿足![]() .
.
(1)求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(2)若![]() ,求
,求![]() 的前n項和
的前n項和![]() ;
;
(3)在(2)的條件下,數(shù)列![]() 是否存在不同的三項構成等比數(shù)列?如果存在,請你求出所有符合題意的項;若不存在,請說明理由.
是否存在不同的三項構成等比數(shù)列?如果存在,請你求出所有符合題意的項;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
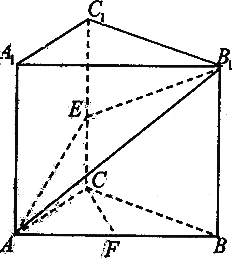
【題目】如圖,直三棱柱![]() 中,
中,![]() 且
且![]() ,
,![]() 是棱
是棱![]() 上的動點,
上的動點,![]() 是
是![]() 的中點.
的中點.
(1)當![]() 是
是![]() 中點時,求證:
中點時,求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角為
所成銳二面角為![]() ,若存在,求
,若存在,求![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com