【題目】如圖，某種螺帽是由一個半徑為2的半球體挖去一個正三棱錐構成的幾何體，該正三棱錐的底面三角形內接于半球底面大圓，頂點在半球面上，則被挖去的正三棱錐體積為_______．
名校課堂系列答案科目：高中數(shù)學 來源： 題型：
【題目】圓錐
（其中
為頂點，
為底面圓心）的側面積與底面積的比是
，則圓錐與它外接球（即頂點在球面上且底面圓周也在球面上）的體積比為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】目前，國內很多評價機構經過反復調研論證，研制出“增值評價”方式。下面實例是某市對“增值評價”的簡單應用，該市教育評價部門對本市
所高中按照分層抽樣的方式抽出
所(其中，“重點高中”
所分別記為
,“普通高中”
所分別記為
),進行跟蹤統(tǒng)計分析，將所高中新生進行了統(tǒng)的入學測試高考后，該市教育評價部門將人學測試成績與高考成績的各校平均總分繪制成了雷達圖.
點表示
學校入學測試平均總分大約
分，
點表示
學校高考平均總分大約
分，則下列敘述不正確的是（ ）
A.各校人學統(tǒng)一測試的成績都在
分以上
B.高考平均總分超過
分的學校有所
C.
學校成績出現(xiàn)負增幅現(xiàn)象
D.“普通高中”學生成績上升比較明顯
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
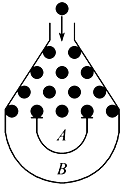
【題目】某超市春節(jié)大酬賓，購物滿100元可參加一次抽獎活動，規(guī)則如下：顧客將一個半徑適當?shù)男∏蚍湃肴鐖D所示的容器正上方的人口處，小球在自由落下的過程中，將3次遇到黑色障礙物，最后落入A袋或B袋中，顧客相應獲得袋子里的獎品.已知小球每次遇到黑色障礙物時，向左向右下落的概率都為
.若活動當天小明在該超市購物消費108元，按照活動規(guī)則，他可參加一次抽獎，則小明獲得A袋中的獎品的概率為_____.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某網購平臺為了解某市居民在該平臺的消費情況，從該市使用其平臺且每周平均消費額超過100元的人員中隨機抽取了100名，并繪制如圖所示頻率分布直方圖，已知中間三組的人數(shù)可構成等差數(shù)列.
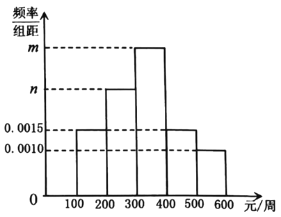
（1）求
的值；
（2）分析人員對100名調查對象的性別進行統(tǒng)計發(fā)現(xiàn)，消費金額不低于300元的男性有20人，低于300元的男性有25人，根據統(tǒng)計數(shù)據完成下列
列聯(lián)表，并判斷是否有
的把握認為消費金額與性別有關？
（3）分析人員對抽取對象每周的消費金額
與年齡
進一步分析，發(fā)現(xiàn)他們線性相關，得到回歸方程
.已知100名使用者的平均年齡為38歲，試判斷一名年齡為25歲的年輕人每周的平均消費金額為多少.（同一組數(shù)據用該區(qū)間的中點值代替）
列聯(lián)表
男性 | 女性 | 合計 | |
消費金額 | |||
消費金額 | |||
合計 |
臨界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
，其中
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，長途車站P與地鐵站O的距離為
千米，從地鐵站O出發(fā)有兩條道路l1，l2，經測量，l1，l2的夾角為45°，OP與l1的夾角
滿足tan＝
（其中0＜θ＜
)，現(xiàn)要經過P修條直路分別與道路l1，l2交匯于A，B兩點，并在A，B處設立公共自行車停放點．
（1）已知修建道路PA，PB的單位造價分別為2m元/千米和m元/千米，若兩段道路的總造價相等，求此時點A，B之間的距離；
（2）考慮環(huán)境因素，需要對OA，OB段道路進行翻修，OA，OB段的翻修單價分別為n元/千米和
n元/千米，要使兩段道路的翻修總價最少，試確定A，B點的位置．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
(a，b
R)．
（1）當a＝b＝1時，求
的單調增區(qū)間；
（2）當a≠0時，若函數(shù)恰有兩個不同的零點，求
的值；
（3）當a＝0時，若
的解集為(m，n)，且(m，n)中有且僅有一個整數(shù)，求實數(shù)b的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的焦點F（1，0），O為坐標原點，A，B是拋物線C上異于 O的兩點．
（1）求拋物線C的方程；
（2）若直線AB過點（8，0），求證：直線OA，OB的斜率之積為定值
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
過點
，且其離心率為
，過坐標原點
作兩條互相垂直的射線與橢圓
分別相交于
，
兩點.
（1）求橢圓的方程；
（2）是否存在圓心在原點的定圓與直線
總相切？若存在，求定圓的方程；若不存在，請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
