
���}Ŀ����D����������![]() �У�
��![]() ����
����![]() �����c(di��n).
�����c(di��n).

��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ����
����![]() �����c(di��n)���������F
�����c(di��n)���������F![]() ���w�e�c������
���w�e�c������![]() ���w�e֮��.
���w�e֮��.
���𰸡���1��Ҋ��������2��![]()
��������
��1���B��AC1��A1C���c(di��n)O���B��OD������λ�������ɵ�OD��BC1���ʶ�BC1��ƽ��A1CD����2������(j��)���F���������w�e��ʽ���ɵó��Y(ji��)Փ��
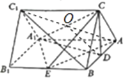
��1���C�����B��AC1��A1C���c(di��n)O���B��OD��
��CC1��AA1��CC1��AA1��
����߅��AA1C1C��ƽ����߅�Σ�
��O��AC1�����c(di��n)����D��AB�����c(di��n)��
��OD��BC1����ODƽ��A1CD��BC1ƽ��A1CD��
��BC1��ƽ��A1CD��
��2���O(sh��)������A1B1C1��ABC�ĸߞ�h���t������A1B1C1��ABC���w�eV��S��ABCh��
��V��V![]() V
V![]() ��V
��V![]() V
V![]() S��ABCh
S��ABCh![]() ��
��
��V![]() ��
��
��CC1��BB1��CC1ƽ��ABB1A1��BB1ƽ��ABB1A1��
��CC1��ƽ��ABB1A1��
��V![]() V
V![]() ��
��
��S![]() S
S![]() ����V
����V![]() V
V![]() ��
��
�������FC��AA1E���w�e�c������A1B1C1��ABC���w�e֮�Ȟ�![]() ��
��


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���O(sh��)
���O(sh��)![]() ����ӈA�A�Ğ�
����ӈA�A�Ğ�![]() .
.

��1����![]() �cֱ��
�cֱ��![]() ���У���(sh��)��(sh��)
���У���(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2���O(sh��)�c(di��n)![]() ��
��![]() �ϣ�ʹ
�ϣ�ʹ![]() ����e����12���c(di��n)
����e����12���c(di��n)![]() ����ֻ������(g��)��ԇ���@�ӵ�
����ֻ������(g��)��ԇ���@�ӵ�![]() �Ƿ���ڣ����������
�Ƿ���ڣ����������![]() �Ę�(bi��o)��(zh��n)���̣��������ڣ��f������.
�Ę�(bi��o)��(zh��n)���̣��������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D�������w�ĵ����c�������w�ĵ�����ͬһƽ����ϣ���AB��CD�������w������(g��)�����ڵ�ƽ���cֱ��CE��EF�ཻ��ƽ��?zh��n)���(sh��)�քeӛ��m��n����ôm+n=�� �� 
A.8
B.9
C.10
D.11
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��С�����Α�ʽ?j��ng)Q���Dž��ӌW(xu��)У�ϳ��F(tu��n)߀�Dž��ӌW(xu��)У�����(du��)���Α�Ҏ(gu��)�t�飺��0�����c(di��n)���ُ�A1 �� A2 �� A3 �� A4 �� A5 �� A6 �� A7 �� A8����D���@8��(g��)�c(di��n)����ȡ���c(di��n)�քe��K�c(di��n)�õ��ɂ�(g��)������ӛ�@�ɂ�(g��)�����Ĕ�(sh��)���e��X����X=0�ͅ��ӌW(xu��)У�ϳ��F(tu��n)����t�ͅ��ӌW(xu��)У�����(du��)�� 
��1����С�����ӌW(xu��)У�ϳ��F(tu��n)�ĸ��ʣ�
��2����X�ķֲ��к͔�(sh��)�W(xu��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞� (����
(����![]() �酢��(sh��)��.�F(xi��n)������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)��.�F(xi��n)������(bi��o)ԭ�c(di��n)��O�c(di��n)�� ![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)��(bi��o)ϵ������
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)��(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1������ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣���2����ֱ��
��ֱ������(bi��o)���̣���2����ֱ��![]() ������
������![]() �صõľ��ε��L(zh��ng)��.
�صõľ��ε��L(zh��ng)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ֱ������(bi��o)ϵ![]() �У��A
���A![]() �c
�c![]() �Sؓ(f��)���S�����c(di��n)
�Sؓ(f��)���S�����c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ,
,![]() �քe�c�A
�քe�c�A![]() ����
����![]() ,
,![]() ���c(di��n)��
���c(di��n)��

��������![]() ,
,![]() ����
����![]() ����e��
����e��
��������ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() ���C����
���C����![]() �鶨ֵ������˶�ֵ��
�鶨ֵ������˶�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=x3+ax2+bx+c�����нY(ji��)Փ���e(cu��)�`���ǣ� ��
A.x����R��f��x����=0
B.����(sh��)y=f��x���ĈD�������Č�(du��)�Q�D��
C.��x����f��x���ĘOСֵ�c(di��n)���tf��x���څ^(q��)�g�����ޣ�x�������{(di��o)�f�p
D.��x����f��x���ĘOֵ�c(di��n)���tf�䣨x����=0
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ֱ����ABC��A1B1C1�У�D��E�քe��AB��BB1�����c(di��n)��AA1=AC=CB= ![]() AB��
AB�� 
��1���C����BC1��ƽ��A1CD
��2��������D��A1C��E������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��������(sh��)f��x��=x2+ax+ ![]() ��������(sh��)���ta��ȡֵ�����ǣ� ��
��������(sh��)���ta��ȡֵ�����ǣ� ��
A.[��1��0]
B.[��1����]
C.[0��3]
D.[3��+��]
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com