【題目】已知定義在（0，+∞）上的函數f（x）的導函數為f'（x），滿足x2f'（x）+xf（x）=lnx，f（e）= 
，則f（x）（ ）
A.有極大值，無極小值
B.有極小值，無極大值
C.既有極大值又有極小值
D.既無極大值也無極小值
科目：高中數學 來源： 題型：
【題目】如果對一切實數x、y，不等式 
﹣cos2x≥asinx﹣ 
恒成立，則實數a的取值范圍是（ ）
A.（﹣∞， 
]
B.[3，+∞）
C.[﹣2 
，2 ]
D.[﹣3，3]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將函數f（x）=cos（ωx+φ）（ω＞0，﹣ 
＜φ＜ ）圖象上每一點的橫坐標伸長為原來的2倍（縱坐標不變），再向右平移 
個單位長度得到y=cosx的圖象，則函數f（x）的單調遞增區間為（ ）
A.[kπ﹣ 
，kπ+ 
]（k∈Z）
B.[kπ﹣ 
，kπ﹣ 
]（k∈Z）
C.[4kπ﹣ 
，kπ﹣ ]（k∈Z）
D.[4kπ﹣ ，kπ+ 
]（k∈Z）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C1的參數方程為 
（t為參數）．以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=2cosθ．
（Ⅰ）把C1的參數方程化為極坐標方程；
（Ⅱ）求C1與C2交點的極坐標（ρ≥0，0≤θ＜2π）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，橢圓C1： 
=1（a＞b＞0）的離心率為 
，x軸被曲線C2：y=x2﹣b截得的線段長等于C1的長半軸長． 
（Ⅰ）求C1 ， C2的方程；
（Ⅱ）設C2與y軸的交點為M，過坐標原點O的直線l與C2相交于點A、B，直線MA，MB分別與C1相交于D，E．
（i）證明：MD⊥ME；
（ii）記△MAB，△MDE的面積分別是S1 ， S2 ． 問：是否存在直線l，使得 
= 
？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在R上的奇函數f（x）和偶函數g（x）滿足f（x）=2g（x）+ 
，若f（ 
）+f（cos2θ）＜f（π）﹣f（ 
），則θ的取值范圍是（ ）
A.（2kπ+ 
，2kπ+ 
），k∈Z
B.（2kπ﹣ ，2kπ）∪（2kπ，2kπ+π）∪（2kπ+π，2kπ+ 
π），k∈Z
C.（2kπ﹣ ，2kπ﹣ ），k∈Z
D.（2kπ﹣ 
，2kπ﹣π）∪（2kπ﹣π，2kπ）∪（2kπ，2kπ+ ），k∈Z
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，以O為極點，x軸的非負半軸為極軸建立極坐標系，已知曲線C：ρsin2θ=2acosθ（a＞0），l：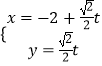 
（t為參數）
（1）求曲線C的普通方程，l的直角坐標方程
（2）設l與C交于M，N兩點，點P（﹣2，0），若|PM|，|MN|，|PN|成等比數列，求實數a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司計劃明年用不超過6千萬元的資金投資于本地養魚場和遠洋捕撈隊．經過本地養魚場年利潤率的調研，得到如圖所示年利潤率的頻率分布直方圖．對遠洋捕撈隊的調研結果是：年利潤率為60%的可能性為0.6，不賠不賺的可能性為0.2，虧損30%的可能性為0.2．假設該公司投資本地養魚場的資金為x（x≥0）千萬元，投資遠洋捕撈隊的資金為y（y≥0）千萬元． 
（1）利用調研數據估計明年遠洋捕撈隊的利潤ξ的分布列和數學期望Eξ．
（2）為確保本地的鮮魚供應，市政府要求該公司對本地養魚場的投資不得低于遠洋捕撈隊的一半．適用調研數據，給出公司分配投資金額的建議，使得明年兩個項目的利潤之和最大．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
