【題目】已知坐標平面上的凸四邊形 ABCD 滿足 
=（1， 
）， 
=（﹣ ，1），則凸四邊形ABCD的面積為； 
的取值范圍是 ．
智趣寒假作業(yè)云南科技出版社系列答案科目：高中數(shù)學 來源： 題型：
【題目】研究函數(shù)f（x）= 
的性質(zhì)，完成下面兩個問題：
①將f（2），f（3），f（5）按從小到大排列為；
②函數(shù)g（x）= 
（x> 0）的最大值為 ．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某化工廠擬建一個下部為圓柱，上部為半球的容器（如圖圓柱高為 
，半徑為 
，不計厚度，單位：米），按計劃容積為 
立方米，且 
，假設(shè)建造費用僅與表面積有關(guān)（圓柱底部不計 ），已知圓柱部分每平方米的費用為2千元，半球部分每平方米的費用為2千元，設(shè)該容器的建造費用為y千元.
（1）求y關(guān)于r的函數(shù)關(guān)系，并求其定義域；
（2）求建造費用最小時的 .
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】若
的部分圖象如圖所示.
（1）求函數(shù)
的解析式；
（2）將
的圖象向左平移
個單位長度得到
的圖象，若
圖象的一個對稱軸為
，求
的最小值；
（3）在第（2）問的前提下，求函數(shù)
在
上的單調(diào)區(qū)間.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列命題：
①若
，則
；
②已知
，
，且
與
的夾角為銳角，則實數(shù)
的取值范圍是
；
③已知
是平面上一定點，
是平面上不共線的三個點，動點
滿足
，
，則的軌跡一定通過
的重心；
④在
中，
，邊長
分別為
，則只有一解；
⑤如果△ABC內(nèi)接于半徑為
的圓，且
則△ABC的面積的最大值
；
其中正確的序號為_______________________。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)f（x）=|ax﹣1|．
（Ⅰ）若f（x）≤2的解集為[﹣6，2]，求實數(shù)a的值；
（Ⅱ）當a=2時，若存在x∈R，使得不等式f（2x+1）﹣f（x﹣1）≤7﹣3m成立，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示，在著名的漢諾塔問題中有三根針和套在一根針上的若干金屬片，按下列規(guī)則，把金屬片從一根針上全部移到另一根針上：①每次只能移動一個金屬片；②在每次移動過程中，每根針上較大的金屬片不能放在較小的金屬片上面．將n個金屬片從1號針移到3號針最少需要移動的次數(shù)記為f（n），則f（6）=（ ） 
A.31
B.33
C.63
D.65
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】《九章算術(shù)》中，將底面為長方形且有一條側(cè)棱與底面垂直的四棱錐稱之為陽馬，將四個面都為直角三角形的四面體稱之為鱉臑．如圖，在陽馬P﹣ABCD中，側(cè)棱PD⊥底面ABCD，且PD=CD，過棱PC的中點E，作EF⊥PB交PB于點F，連接DE，DF，BD，BE．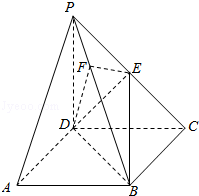 
（1）證明：PB⊥平面DEF．試判斷四面體DBEF是否為鱉臑，若是，寫出其每個面的直角（只需寫出結(jié)論）；若不是，說明理由；
（2）若面DEF與面ABCD所成二面角的大小為 
，求 
的值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
