
【題目】十九大指出中國的電動汽車革命早已展開,通過以新能源汽車替代汽/柴油車,中國正在大力實施一項將重塑全球汽車行業的計劃.2019年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本2500萬元,每生產x(百輛),需另投入成本![]() 萬元,且
萬元,且 .由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
.由市場調研知,每輛車售價5萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2019年的利潤![]() (萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額-成本)
(萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額-成本)
(2)2019年產量為多少百輛時,企業所獲利潤最大?并求出最大利潤.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知ABCD—A′B′C′D′是平行六面體.
(1)化簡![]() ;
;
(2)設M是底面ABCD的中心,N是側面BC C′ B′對角線B C′上的![]() 分點,設
分點,設![]() ,試求α,β,γ的值.
,試求α,β,γ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右頂點為A,上頂點為B.已知橢圓的離心率為
的右頂點為A,上頂點為B.已知橢圓的離心率為![]() ,
,![]() .
.
(1)求橢圓的方程;
(2)設直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,
兩點,![]() 與直線
與直線![]() 交于點M,且點P,M均在第四象限.若
交于點M,且點P,M均在第四象限.若![]() 的面積是
的面積是![]() 面積的2倍,求
面積的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣kx+k.
(Ⅰ)若f(x)≥0有唯一解,求實數k的值;
(Ⅱ)證明:當a≤1時,x(f(x)+kx﹣k)<ex﹣ax2﹣1.
(附:ln2≈0.69,ln3≈1.10, ![]() ,e2≈7.39)
,e2≈7.39)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上有最大值4 和最小值1,設
上有最大值4 和最小值1,設![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在區間
在區間![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某大型水上樂園內有一塊矩形場地![]() 米,
米, ![]() 米,以
米,以![]() 為直徑的半圓
為直徑的半圓![]() 和半圓
和半圓![]() (半圓在矩形
(半圓在矩形![]() 內部)為兩個半圓形水上主題樂園,
內部)為兩個半圓形水上主題樂園, ![]() 都建有圍墻,游客只能從線段
都建有圍墻,游客只能從線段![]() 處進出該主題樂園.為了進一步提高經濟效益,水上樂園管理部門決定沿著
處進出該主題樂園.為了進一步提高經濟效益,水上樂園管理部門決定沿著![]() 修建不銹鋼護欄,沿著線段
修建不銹鋼護欄,沿著線段![]() 修建該主題樂園大門并設置檢票口,其中
修建該主題樂園大門并設置檢票口,其中![]() 分別為
分別為![]() 上的動點,
上的動點, ![]() ,且線段
,且線段![]() 與線段
與線段![]() 在圓心
在圓心![]() 和
和![]() 連線的同側.已知弧線部分的修建費用為
連線的同側.已知弧線部分的修建費用為![]() 元/米,直線部門的平均修建費用為
元/米,直線部門的平均修建費用為![]() 元/米.
元/米.

(1)若![]() 米,則檢票等候區域(其中陰影部分)面積為多少平方米?
米,則檢票等候區域(其中陰影部分)面積為多少平方米?
(2)試確定點![]() 的位置,使得修建費用最低.
的位置,使得修建費用最低.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】參與舒城中學數學選修課的同學對某公司的一種產品銷量與價格進行了統計,得到如下數據和散點圖.
定價x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年銷量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

參考數據:
![]() ,
,
![]() .
.
(1)根據散點圖判斷y與x,z與x哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
(2)根據(1)的判斷結果及數據,建立y關于x的回歸方程(方程中的系數均保留兩位有效數字).
(3)當定價為150元/千克時,試估計年銷量.
附:對于一組數據(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回歸直線![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估計分別為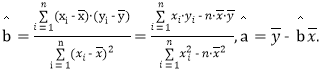
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com