
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,
, ![]() 、
、![]() 分別是它的左、右焦點,且存在直線
分別是它的左、右焦點,且存在直線![]() ,使
,使![]() 、
、![]() 關于
關于![]() 的對稱點恰好是圓
的對稱點恰好是圓![]() :
: ![]()
![]() (
(![]() ,
, ![]() )的一條直徑的兩個端點.
)的一條直徑的兩個端點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與拋物線
與拋物線![]() (
(![]() )相交于
)相交于![]() 、
、![]() 兩點,射線
兩點,射線![]() 、
、![]() 與橢圓
與橢圓![]() 分別相交于點
分別相交于點![]() 、
、![]() .試探究:是否存在數集
.試探究:是否存在數集![]() ,當且僅當
,當且僅當![]() 時,總存在
時,總存在![]() ,使點
,使點![]() 在以線段
在以線段![]() 為直徑的圓內?若存在,求出數集
為直徑的圓內?若存在,求出數集![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)見解析.
; (Ⅱ)見解析.
【解析】試題分析:(Ⅰ)橢圓的焦距![]() 等于圓
等于圓![]() 的直徑,所以
的直徑,所以![]() ,根據離心率求出
,根據離心率求出![]() ;
;
(Ⅱ)因為![]() 、
、![]() 關于
關于![]() 的對稱點恰好是圓
的對稱點恰好是圓![]() 的一條直徑的兩個端點,所以直線
的一條直徑的兩個端點,所以直線![]() 是線段
是線段![]() 的垂直平分線(
的垂直平分線(![]() 是坐標原點),故
是坐標原點),故![]() 方程為
方程為![]() ,與
,與![]() 聯立得:
聯立得: ![]() ,點
,點![]() 在以線段
在以線段![]() 為直徑的圓內
為直徑的圓內![]()
![]()
![]()
![]() 韋達定理代入求解即可.
韋達定理代入求解即可.
試題解析:
(Ⅰ)將圓![]() 的方程配方得:
的方程配方得: ![]() ,所以其圓心為
,所以其圓心為![]() ,半徑為2.
,半徑為2.
由題設知,橢圓的焦距![]() 等于圓
等于圓![]() 的直徑,所以
的直徑,所以![]() ,
,
又![]() ,所以
,所以![]() ,從而
,從而![]() ,故橢圓
,故橢圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)因為![]() 、
、![]() 關于
關于![]() 的對稱點恰好是圓
的對稱點恰好是圓![]() 的一條直徑的兩個端點,所以直線
的一條直徑的兩個端點,所以直線![]() 是線段
是線段![]() 的垂直平分線(
的垂直平分線(![]() 是坐標原點),故
是坐標原點),故![]() 方程為
方程為![]() ,與
,與![]() 聯立得:
聯立得: ![]() ,由其判別式
,由其判別式![]() 得
得![]() ,①
,①
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
從而![]()
![]() ,
, 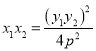
![]() .
.
因為![]() 的坐標為
的坐標為![]() ,所以
,所以![]() ,
, ![]() .
.
注意到![]() 與
與![]() 同向,
同向, ![]() 與
與![]() 同向,所以
同向,所以
點![]() 在以線段
在以線段![]() 為直徑的圓內
為直徑的圓內![]()
![]()
![]()
![]()
![]()
![]() ,②
,②
當且僅當![]()
![]() 即
即![]() 時,總存在
時,總存在![]() ,使②成立.
,使②成立.
又當![]() 時,由韋達定理知方程
時,由韋達定理知方程![]()
![]() 的兩根均為正數,故使②成立的
的兩根均為正數,故使②成立的![]() ,從而滿足①.
,從而滿足①.
故存在數集![]() ,當且僅當
,當且僅當![]() 時,總存在
時,總存在![]() ,使點
,使點![]() 在以線段
在以線段![]() 為直徑的圓內.
為直徑的圓內.


科目:高中數學 來源: 題型:
【題目】(本小題滿分8分) 已知拋物線C:y=-x2+4x-3 .
(1)求拋物線C在點A(0,-3)和點B(3,0)處的切線的交點坐標;
(2)求拋物線C與它在點A和點B處的切線所圍成的圖形的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①函數 ![]() 是奇函數;
是奇函數;
②存在實數x,使sinx+cosx=2;
③若α,β是第一象限角且α<β,則tanα<tanβ;
④ ![]() 是函數
是函數 ![]() 的一條對稱軸;
的一條對稱軸;
⑤函數 ![]() 的圖象關于點
的圖象關于點 ![]() 成中心對稱.
成中心對稱.
其中正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】咖啡館配制兩種飲料,甲種飲料分別用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙種飲料分別用奶粉
。乙種飲料分別用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限額為奶粉
。已知每天使用原料限額為奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲種飲料每杯能獲利
。如果甲種飲料每杯能獲利![]() 元,乙種飲料每杯能獲利
元,乙種飲料每杯能獲利![]() 元。每天在原料的使用限額內飲料能全部售出,每天應配制兩種飲料各多少杯能獲利最大?
元。每天在原料的使用限額內飲料能全部售出,每天應配制兩種飲料各多少杯能獲利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列五個命題:①“若![]() ,則
,則![]() 或
或![]() ”是假命題;②從正方體的面對角線中任取兩條作為一對,其中所成角為
”是假命題;②從正方體的面對角線中任取兩條作為一對,其中所成角為![]() 的有48對;③“
的有48對;③“ ![]() ”是方程
”是方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線的充分不必要條件;④點
軸上的雙曲線的充分不必要條件;④點![]() 是曲線
是曲線![]() (
(![]() ,
, ![]() )上的動點,且滿足
)上的動點,且滿足![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]() ;⑤若隨機變量
;⑤若隨機變量![]() 服從正態分布
服從正態分布![]() ,且
,且![]() ,則
,則![]() .其中正確命題的序號是__________(請把正確命題的序號填在橫線上).
.其中正確命題的序號是__________(請把正確命題的序號填在橫線上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形OQRP為矩形,其中P,Q分別是函數f(x)= ![]() sinwx(A>0,w>0)圖象上的一個最高點和最低點,O為坐標原點,R為圖象與x軸的交點.
sinwx(A>0,w>0)圖象上的一個最高點和最低點,O為坐標原點,R為圖象與x軸的交點. 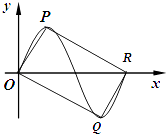
(1)求f(x)的解析式
(2)對于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四個不同的實數根,求實數a的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貨輪勻速行駛在相距![]() 海里的甲、乙兩地間運輸貨物,運輸成本由燃料費用和其他費用組成.已知該貨輪每小時的燃料費用與其航行速度的平方成正比(比例系數為
海里的甲、乙兩地間運輸貨物,運輸成本由燃料費用和其他費用組成.已知該貨輪每小時的燃料費用與其航行速度的平方成正比(比例系數為![]() ),其他費用為每小時
),其他費用為每小時![]() 元,且該貨輪的最大航行速度為
元,且該貨輪的最大航行速度為![]() 海里/小時.
海里/小時.
(1)請將從甲地到乙地的運輸成本![]() (元)表示為航行速度
(元)表示為航行速度![]() (海里/小時)的函數;
(海里/小時)的函數;
(2)要使從甲地到乙地的運輸成本最少,該貨輪應以多大的航行速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求![]() 的值;
的值;
(2)將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位,再將得到的圖像上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數
個單位,再將得到的圖像上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數![]() 的圖像,求函數
的圖像,求函數![]() 的單調遞減區間.
的單調遞減區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com