
���}Ŀ��ƽ���ϵăɂ�����![]() ��
��![]() �M��
�M��![]() ��
��![]() ����
����![]() ��
��![]() .����
.����![]() ����
���� .
.
��1������c![]() �龀��
�龀��![]() �����c�����C:
�����c�����C: ![]() ��
��
��2����![]() �����ֵ������˕r��߅��
�����ֵ������˕r��߅��![]() ��e�����ֵ.
��e�����ֵ.
���𰸡���1���C��Ҋ��������2��![]() ��
��![]() ��
��
��������
ԇ�}��������1��������c![]() �龀��
�龀��![]() �����c������
�����c������![]() ���Bͬ��֪����
���Bͬ��֪����![]() �����C������2���O(sh��)�c
�����C������2���O(sh��)�c![]() �龀��
�龀��![]() �����c���t��
�����c���t��![]() ��֪
��֪![]() �����ɣ�1�����}�O(sh��)�l����
�����ɣ�1�����}�O(sh��)�l����![]() ���Ķ����Д�
���Ķ����Д�![]() ��
��![]() ��
��![]() ��
��![]() ���c������
���c������![]() ��A�ġ�
��A�ġ�![]() ��돽�ĈA�ϣ���֪
��돽�ĈA�ϣ���֪![]() ��A
��A![]() ��ֱ�����õ�
��ֱ�����õ�![]() �������û�������ʽ�����������߅����e�����ֵ.
�������û�������ʽ�����������߅����e�����ֵ.
ԇ�}��������1���C��������c![]() �龀��
�龀��![]() �����c��
�����c��
����![]() .
.
����![]() .
.
��2���⣺�O(sh��)�c![]() �龀��
�龀��![]() �����c��
�����c��
�t��![]() ��֪
��֪![]() .
.
���ɣ�1���� ����
����
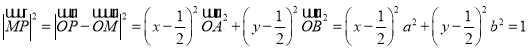
����![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() ���c������
���c������![]() ��A�ġ�
��A�ġ�![]() ��돽�ĈA�ϣ�
��돽�ĈA�ϣ�
���Ԯ�(d��ng)�҃H��(d��ng)![]() ��A
��A![]() ��ֱ���r��
��ֱ���r��![]() .
.
�@�r��߅��![]() ����Σ�
�����
�t![]() ��
��
��(d��ng)�҃H��(d��ng)![]() �r����߅��
�r����߅��![]() ����e������ֵ��
����e������ֵ��![]() .
.


 ������I(y��)���������ϵ�д�
������I(y��)���������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ƽ��ֱ������(bi��o)ϵ![]() �У��E�A
�У��E�A![]() ���ҽ��c��
���ҽ��c��![]() ���x����
���x����![]() ���^�c
���^�c![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() �S��ֱ�����E�A
�S��ֱ�����E�A![]() �صõ����L��1.
�صõ����L��1.
��������E�A![]() �ķ��̣�
�ķ��̣�
������ӛ�E�A![]() ����,����c�քe��A,B���O(sh��)�^�c
����,����c�քe��A,B���O(sh��)�^�c![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() �քe�����c
�քe�����c![]() �����C��ֱ��
�����C��ֱ��![]() �ض��^һ���c������ԓ���c������(bi��o).
�ض��^һ���c������ԓ���c������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���㷨��ָ������Ӌ��C(j��)����Q��ijһ��}�ij�����E����������
A. ������ B. ���_��
C. ���� D. �o����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������D��ʾ�Ŀ��g���w�У�ƽ��ACD��ƽ��ABC����ACD�c��ACB��߅�L��2�ĵ�߅�����Σ�BE=2��BE��ƽ��ABC���ɵĽǞ�60�������cE��ƽ��ABC�ϵ���Ӱ����![]() ��ƽ�־���.
��ƽ�־���.

��1�����C��DE��ƽ��ABC��
��2����˿��g���w���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() �M��
�M��![]() ��
��![]() ������
������![]() ��
��
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ���dž��{(di��o)����(sh��)����(sh��)
���dž��{(di��o)����(sh��)����(sh��)![]() ��ȡֵ������
��ȡֵ������
��3�����P(gu��n)��![]() �ķ���
�ķ���![]() �Ѕ^(q��)�g
�Ѕ^(q��)�g![]() ����һ�����c����(sh��)
����һ�����c����(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����³����\�к��ݔ���Y(ji��)����
i=1
WHILE i<8
i=i+2
S=2*i+3
i=i�C1
WEND
PRINT S
END
A. 17 B. 19 C. 21 D. 23
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�dȤС�M���{(di��o)�鮔(d��ng)?sh��)ؾ��������ˮƽ���������?d��ng)?sh��)�һ����5000�˵���^(q��)�S�C(j��)��ȡ1000�ˣ��{(di��o)�������������룬����(j��)���Ô�(sh��)��(j��)���˘ӱ����l�ʷֲ�ֱ���D��ÿ���ֽM��������c���������Ҷ��c�����һ�M��ʾ������[1000��1500������������ˆT������δ��(bi��o)������M픲�����(y��ng)�Ŀv�S��(sh��)��(j��)��
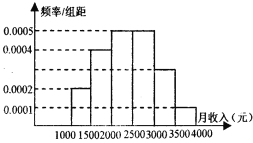
������Ո���a�ϵ���M픲�����(y��ng)�Ŀv�S��(sh��)��(j��)��������ԓ��^(q��)������������[3000��4000�����˔�(sh��)��
����������(j��)�l�ʷֲ�ֱ���D����ӱ���(sh��)��(j��)����λ��(sh��)��
���������˷�������������c���g���I(y��)�ȷ�����P(gu��n)ϵ����횰��������ُ��@1000�����÷ӳ�ӷ������100�����M(j��n)һ���������t��������[2500��3000�����@�Α�(y��ng)�������?
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����б������_���ǣ� ��
�ٚw�{�����������һ��������������[��������һ�㵽�����������
��������������һ����������ܷ�������һ�N�g���C������
A. �ڢ� B. �٢� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ����
����
��1��������(sh��)![]() ���ژO��ֵ�͘OСֵ����
���ژO��ֵ�͘OСֵ����![]() ��ȡֵ������
��ȡֵ������
��2���O(sh��)![]() ��
��![]() �քe��
�քe��![]() �ĘO��ֵ�͘OСֵ�������ڌ���(sh��)
�ĘO��ֵ�͘OСֵ�������ڌ���(sh��) ��ʹ��
��ʹ��![]() ����
����![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com