Question

【題目】已知函數(shù)f（x）= + ．
（1）求函數(shù)f（x）的定義域和值域；
（2）設(shè)F（x）= [f2（x）﹣2]+f（x）（a為實數(shù)），求F（x）在a＜0時的最大值g（a）；
（3）對（2）中g(shù)（a），若﹣m2+2tm+ ≤g（a）對a＜0所有的實數(shù)a及t∈[﹣1，1]恒成立，求實數(shù)m的取值范圍．

Answer 1

【答案】
（1）解：由1+x≥0且1﹣x≥0，得﹣1≤x≤1，

所以函數(shù)的定義域為[﹣1，1]，

又[f（x）]2=2+2 ∈[2，4]，由f（x）≥0，得f（x）∈[ ，2]，

所以函數(shù)值域為[ ，2]

（2）解：因為F（x）= =a + + ，

令t=f（x）= + ，則 = ﹣1，

∴F（x）=m（t）=a（ ﹣1）+t= ，t∈[ ，2]，

由題意知g（a）即為函數(shù)m（t）= ，t∈[ ，2]的最大值．

注意到直線t=﹣ 是拋物線m（t）= 的對稱軸．

因為a＜0時，函數(shù)y=m（t），t∈[ ，2]的圖象是開口向下的拋物線的一段，

①若t=﹣ ∈（0， ]，即a≤﹣ ，則g（a）=m（ ）= ；

②若t=﹣ ∈（ ，2]，即﹣ ＜a≤﹣ ，則g（a）=m（﹣ ）=﹣a﹣ ；

③若t=﹣ ∈（2，+∞），即﹣ ＜a＜0，則g（a）=m（2）=a+2，

綜上有g(shù)（a）=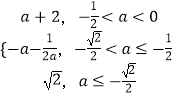

（3）解：易得 ，

由﹣ ≤g（a）對a＜0恒成立，即要使﹣ ≤gmin（a）= 恒成立，

m2﹣2tm≥0，令h（t）=﹣2mt+m2，對所有的t∈[﹣1，1]，h（t）≥0成立，

只需 ，

解得m的取值范圍是m≤﹣2或m=0，或m≥2

【解析】（1）由1+x≥0且1﹣x≥0可求得定義域，先求[f（x）]2的值域，再求f（x）的值域；（2）F（x）=a + + ，令t=f（x）= + ，則 = ﹣1，由此可轉(zhuǎn)化為關(guān)于t的二次函數(shù)，按照對稱軸t=﹣ 與t的范圍[ ，2]的位置關(guān)系分三種情況討論，借助單調(diào)性即可求得其最大值；（3）先由（2）求出函數(shù)g（x）的最小值，﹣ ≤g（a）對a＜0恒成立，即要使﹣ ≤gmin（a）恒成立，從而轉(zhuǎn)化為關(guān)于t的一次不等式，再根據(jù)一次函數(shù)的單調(diào)性可得不等式組，解出即可．