
為了解某班學生喜愛打籃球是否與性別有關,對該班50名學生進行了問卷調查,得到了如下的2×2列聯表:
| 喜愛打籃球 | 不喜愛打籃球 | 總計 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
總計 | 30 | 20 | 50 |
則在犯錯誤的概率不超過 的前提下認為喜愛打籃球與性別有關(請用百分數表示).
附:χ2=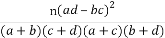
P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十四選修4-2第一節練習卷(解析版) 題型:解答題
已知曲線C1:x2+y2=1,對它先作矩陣A=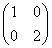 對應的變換,再作矩陣B=
對應的變換,再作矩陣B=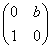 對應的變換得到曲線C2:
對應的變換得到曲線C2: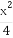 +y2=1,求實數b的值.
+y2=1,求實數b的值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十二第十章第九節練習卷(解析版) 題型:解答題
甲、乙兩運動員進行射擊訓練,已知他們擊中目標的環數都穩定在7,8,9,10環,且每次射擊成績互不影響,射擊環數的頻率分布表如下:
甲運動員
射擊環數 | 頻數 | 頻率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合計 | 100 | 1 |
乙運動員
射擊環數 | 頻數 | 頻率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合計 | 80 | 1 |
若將頻率視為概率,回答下列問題:
(1)求甲運動員射擊1次擊中10環的概率.
(2)求甲運動員在3次射擊中至少有1次擊中9環以上(含9環)的概率.
(3)若甲運動員射擊2次,乙運動員射擊1次,ξ表示這3次射擊中擊中9環以上(含9環)的次數,求ξ的分布列及E(ξ).
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十九選修4-5第一節練習卷(解析版) 題型:解答題
設函數f(x)=|2x-1|+|2x-3|,x∈R.
(1)求關于x的不等式f(x)≤5的解集.
(2)若g(x)=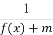 的定義域為R,求實數m的取值范圍.
的定義域為R,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十三第十章第十節練習卷(解析版) 題型:選擇題
通過隨機詢問110名性別不同的行人,對過馬路是愿意走斑馬線還是愿意走人行天橋進行抽樣調查,得到如下的2×2列聯表:
| 男 | 女 | 總計 |
走天橋 | 40 | 20 | 60 |
走斑馬線 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由χ2= 算得,
算得,
χ2= ≈7.8.
≈7.8.
以下結論正確的是( )
(A)有99%以上的把握認為“選擇過馬路的方式與性別有關”
(B)有99%以上的把握認為“選擇過馬路的方式與性別無關”
(C)在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別有關”
(D)在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別無關”
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十三第十章第十節練習卷(解析版) 題型:選擇題
下面是2×2列聯表:
| y1 | y2 | 總計 |
x1 | a | 21 | 73 |
x2 | 22 | 25 | 47 |
總計 | b | 46 | 120 |
則表中a,b的值分別為( )
(A)94,72 (B)52,50
(C)52,74 (D)74,52
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數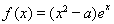 .
.
(Ⅰ)若函數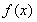 在
在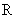 上不是單調函數,求實數
上不是單調函數,求實數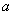 的取值范圍;
的取值范圍;
(Ⅱ)當 時,討論函數
時,討論函數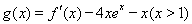 的零點個數.
的零點個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com