
【題目】在平面直角坐標系![]() 中,已知
中,已知![]() 是曲線
是曲線![]() (
(![]() 為參數(shù))上的動點,將
為參數(shù))上的動點,將![]() 繞點
繞點![]() 順時針旋轉(zhuǎn)90°得到
順時針旋轉(zhuǎn)90°得到![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,直線![]() 與曲線
與曲線![]() 分別相交于異于極點
分別相交于異于極點![]() 的
的![]() 兩點,點
兩點,點![]() ,當
,當![]() 時,求直線
時,求直線![]() 的斜率.
的斜率.
 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 經(jīng)過點M(﹣2,﹣1),離心率為
經(jīng)過點M(﹣2,﹣1),離心率為![]() .過點M作傾斜角互補的兩條直線分別與橢圓C交于異于M的另外兩點P、Q.
.過點M作傾斜角互補的兩條直線分別與橢圓C交于異于M的另外兩點P、Q.
(Ⅰ)求橢圓C的方程;
(Ⅱ)試判斷直線PQ的斜率是否為定值,證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了提高生產(chǎn)線的運行效率,工廠對生產(chǎn)線的設備進行了技術(shù)改造.為了對比技術(shù)改造后的效果,采集了生產(chǎn)線的技術(shù)改造前后各20次連續(xù)正常運行的時間長度(單位:天)數(shù)據(jù),并繪制了如下莖葉圖:
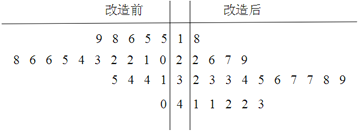
(Ⅰ)(1)設所采集的40個連續(xù)正常運行時間的中位數(shù)![]() ,并將連續(xù)正常運行時間超過
,并將連續(xù)正常運行時間超過![]() 和不超過
和不超過![]() 的次數(shù)填入下面的列聯(lián)表:
的次數(shù)填入下面的列聯(lián)表:
超過 | 不超過 | |
改造前 |
|
|
改造后 |
|
|
試寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根據(jù)(1)中的列聯(lián)表,能否有![]() 的把握認為生產(chǎn)線技術(shù)改造前后的連續(xù)正常運行時間有差異?
的把握認為生產(chǎn)線技術(shù)改造前后的連續(xù)正常運行時間有差異?
附: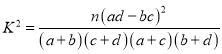 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工廠的生產(chǎn)線的運行需要進行維護.工廠對生產(chǎn)線的生產(chǎn)維護費用包括正常維護費、保障維護費兩種對生產(chǎn)線設定維護周期為![]() 天(即從開工運行到第
天(即從開工運行到第![]() 天(
天(![]() )進行維護.生產(chǎn)線在一個生產(chǎn)周期內(nèi)設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內(nèi),若生產(chǎn)線能連續(xù)運行,則不會產(chǎn)生保障維護費;若生產(chǎn)線不能連續(xù)運行,則產(chǎn)生保障維護費.經(jīng)測算,正常維護費為0.5萬元
)進行維護.生產(chǎn)線在一個生產(chǎn)周期內(nèi)設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內(nèi),若生產(chǎn)線能連續(xù)運行,則不會產(chǎn)生保障維護費;若生產(chǎn)線不能連續(xù)運行,則產(chǎn)生保障維護費.經(jīng)測算,正常維護費為0.5萬元![]() 次;保障維護費第一次為0.2萬元
次;保障維護費第一次為0.2萬元![]() 周期,此后每增加一次則保障維護費增加0.2萬元.現(xiàn)制定生產(chǎn)線一個生產(chǎn)周期(以120天計)內(nèi)的維護方案:
周期,此后每增加一次則保障維護費增加0.2萬元.現(xiàn)制定生產(chǎn)線一個生產(chǎn)周期(以120天計)內(nèi)的維護方案:![]() ,
,![]() ,2,3,4.以生產(chǎn)線在技術(shù)改造后一個維護周期內(nèi)能連續(xù)正常運行的頻率作為概率,求一個生產(chǎn)周期內(nèi)生產(chǎn)維護費的分布列及期望值.
,2,3,4.以生產(chǎn)線在技術(shù)改造后一個維護周期內(nèi)能連續(xù)正常運行的頻率作為概率,求一個生產(chǎn)周期內(nèi)生產(chǎn)維護費的分布列及期望值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左,右焦點,
的左,右焦點,![]() 兩點分別是橢圓
兩點分別是橢圓![]() 的上,下頂點,
的上,下頂點,![]() 是等腰直角三角形,延長
是等腰直角三角形,延長![]() 交橢圓
交橢圓![]() 于
于![]() 點,且
點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的動點,直線
的動點,直線![]() 與直
與直![]() 分別相交于
分別相交于![]() 兩點,點
兩點,點![]() ,求證:
,求證:![]() 的外接圓恒過原點
的外接圓恒過原點![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校甲、乙、丙、丁四個專業(yè)分別有150,150,400,300名學生.為了解學生的就業(yè)傾向,用分層抽樣的方法從該校這四個專業(yè)中抽取60名學生進行調(diào)查,則應從丁專業(yè)抽取的學生人數(shù)為____.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖是九江市2019年4月至2020年3月每月最低氣溫與最高氣溫(℃)的折線統(tǒng)計圖:已知每月最低氣溫與最高氣溫的線性相關(guān)系數(shù)r=0.83,則下列結(jié)論錯誤的是( )
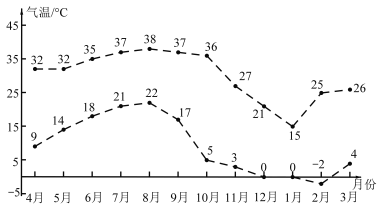
A.每月最低氣溫與最高氣溫有較強的線性相關(guān)性,且二者為線性正相關(guān)
B.月溫差(月最高氣溫﹣月最低氣溫)的最大值出現(xiàn)在10月
C.9﹣12月的月溫差相對于5﹣8月,波動性更大
D.每月最高氣溫與最低氣溫的平均值在前6個月逐月增加
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com